|
La trasformazione dipende dai 6 parametri a, b, c, d,
e, f;
x e y rappresentano rispettivamente
l'ascissa e l'ordinata del punto di partenza, mentre x' e y'
rappresentano quelle del punto trasformato.
SIMILITUDINE
Si tratta di una affinità in cui risulta costante il rapporto di segmenti corrispondenti. Indichiamo con k tale rapporto costante, che nelle similitudini viene sempre considerato positivo. Risolviamo ora il seguente problema:
Dati due segmenti AB ed A'B' tali che A'B'/AB = k, vogliamo trovare il corrispondente di un qualsiasi punto C del piano in modo tale che i triangoli ABC ed A'B'C' risultino simili e quindi tali che il rapporto di due loro lati corrispondenti sia sempre k.
Abbiamo due soluzioni:
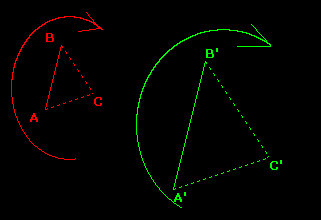 |  |
Similitudine diretta:
il verso di percorrenza dei vertici si mantiene |
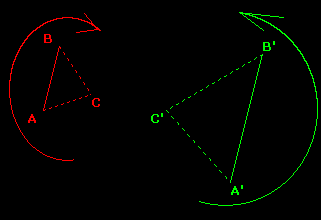
Similitudine indiretta o invertente:
il verso di percorrenza dei vertici si inverte |
Dunque per stabilire una similitudine è sufficiente conoscere il rapporto k > 0 di due segmenti corrispondenti e sapere se essa è diretta o indiretta.
|