La trasformazione dipende dai 6 parametri a, b, c, d, e, f;
x e y rappresentano rispettivamente l'ascissa e l'ordinata del punto di partenza, mentre x' e y' rappresentano quelle del punto trasformato.
Studiamone alcuni casi particolari, supponendo sempre che risulti ae-bd diverso da 0.
PRIMO CASO x'= ax
y'= ey
Si tratta di variazioni di scala, in generale diverse, lungo i due assi;
ad esempio
x'= 3x
y'= 0.5y
SECONDO CASO (Particolare del primo)
x'= ax
y'= ay
Si tratta della stessa variazione di
scala lungo i due assi, detta omotetia;
ad esempio
x'= 2x
y'= 2y
ESEMPIO
| 
|
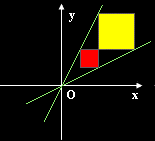
L'origine resta unita (cioè corrisponde a se stessa): essa viene detta il centro dell'omotetia perché è il punto d'incontro di tutte le rette che uniscono punti corrispondenti.
Anche gli assi restano uniti, ma i loro punti no: sia le ascisse che le
ordinate si raddoppiano.
|
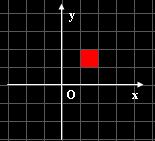
Il reticolato di partenza |
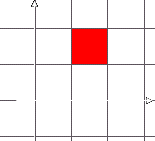
x'=2x;y'=2y
|
In
conclusione, il reticolato a quadretti di lato unitario della prima immagine
si trasforma nel reticolato della seconda immagine, che è sempre a maglie
quadrate.
Nell'omotetia, dunque, segmenti corrispondenti sono sempre in proporzione.
| |
|