|
Vogliamo dunque trovare la più generale trasformazione nel piano che trasformi rette parallele in rette parallele. Come fare?
Indichiamo con P' il punto corrispondente a P nella trasformazione.
Innanzitutto osserviamo che la trasformazione è una corrispondenza biunivoca, perciò:
- se P appartiene ad una retta r, il suo trasformato P' appartiene alla trasformata r' di r;
- se due figure hanno un punto A di intersezione, le figure trasformate si intersecano nel punto A', trasformato di A
- la trasformazione è invertibile.
Quindi basta cercare una trasformazione che trasformi una retta in una retta per essere certi che la stessa trasformazione trasforma rette parallele in rette parallele.
Infatti:
- se due rette r ed s sono parallele e distinte non hanno alcun punto di intersezione;
- se per assurdo le rette trasformate r' ed s' avessero un punto di intersezione P' questo dovrebbe essere il trasformato di un punto P appartenente sia ad r che ad s, che quindi non sarebbero parallele e distinte.
CHIAMIAMO AFFINITA' UNA TRASFORMAZIONE GEOMETRICA NEL PIANO CHE MUTA UNA RETTA IN UNA RETTA: QUESTA DI SICURO
TRASFORMA RETTE PARALLELE IN RETTE PARALLELE.
DIMOSTRAZIONE
Visto che ad una retta deve corrispondere una retta, la trasformazione l'equazione più generale potrebbe essere
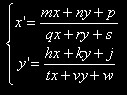
La nostra equazione però deve
risultare biunivoca e dunque i denominatori devono risultare diversi da zero,
altrimenti ci sono dei punti che non hanno alcun punto corrispondente: questo
avviene soltanto se q = r = t = v = 0, mentre s e w devono
essere diversi da zero; ecco dunque l'equazione dell'affinità: |
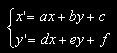 | con | 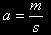 | e così via. |
| |
|
|
Visto che la trasformazione deve essere invertibile, il sistema deve essere determinato. I coefficienti delle incognite x ed y perciò non devono essere in proporzione, e quindi:
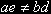 . .
Si dimostra che ogni sistema lineare di questo tipo individua una affinità; al
variare dei coefficienti a, b, c, d, e, f, si ottengono particolari affinità,
come ad esempio le isometrie o le similitudini.
ESEMPIO
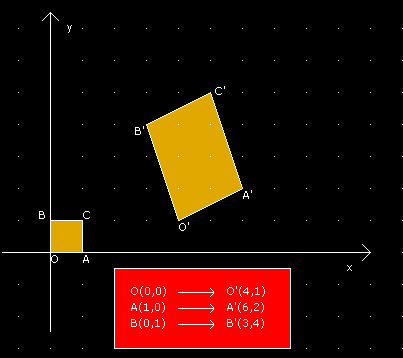
Scriviamo l'equazione della trasformazione in figura. Allo scopo determiniamo i coefficienti del sistema imponendo che ad O corrisponda O', ad A corrisponda A', a B corrisponda B', tenendo anche conto della seguente, importante considerazione:
non è necessario trasformare tutti e quattro i vertici del quadrato infatti ad
esso deve corrispondere un parallelogramma.
Ora, un parallelogramma è determinato univocamente non appena si conoscano tre
suoi vertici consecutivi dati in un ordine assegnato.
Dati tre vertici ABC, nell'ordine scritto, il quarto vertice si trova, ad
esempio, come intersezione della parallela al lato BC passante per A con la
parallela al lato AB passante per C.
Si ottiene il sistema
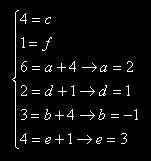 | e sostituendo si ha | 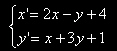
| 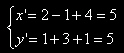
Verifichiamo poi che, nella trasformazione così trovata, a C(1,1) corrisponde C'(5,5) e che, in effetti, il quadrato si è trasformato in parallelogramma.
|
| |
|
| |