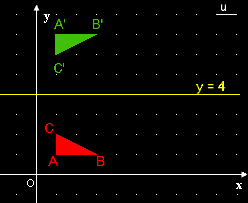Nell'esempio si vede come due punti corrispondenti hanno la stessa ascissa, mentre la somma delle ordinate è costante. Ogni segmento AB ed il suo corrispondente A'B' sono congruenti (si tratta di un'isometria); se A ed A' sono punti corrispondenti, essi appartengono sempre a semipiani opposti rispetto all'asse di simmetria, che è anche l'unica retta di punti uniti; sono poi unite le rette che uniscono punti corrispondenti, e che sono perpendicolari all'asse di simmetria. Non vi sono altre rette unite. Se poi una retta, ad esempio AB, è parallela all'asse di simmetria, essa si trasforma in una retta (nell'esempio A'B') pure parallela all'asse di simmetria; se invece la retta (ad esempio BC) non ha la stessa direzione dell'asse di simmetria, allora essa e la sua corrispondente di intersecano in punto appartenente al suddetto asse. Notiamo infine che di tratta di un' isometria inversa, che cioè ribalta le figure; essa, applicata due volte di seguito, dà luogo all'identità: si tratta di una trasformazione involutoria.