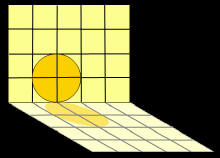Le ombre con il passare delle ore si accorciano, si allungano, cambiano direzione... ma mantengono fisse alcune proprietà dell'oggetto che le genera, già osservate in tempi remoti.
Nella figura abbiamo schematizzato una finestra con sbarre di protezione in cui è inserita una forma circolare. Questi oggetti proiettano le loro ombre su uno stesso piano. Osserviamo che:

• in particolare la finestra, che racchiude 20 quadrati tutti uguali tra di loro, si è trasformata in un parallelogramma che racchiude 20 parallelogrammi uguali tra di loro; dunque possiamo intuire che resta costante il rapporto fra le aree di figure corrispondenti.

Che cosa è una trasformazione geometrica?
Per semplicità riferiamoci ad un piano. Si tratta di creare una legge che ci consenta di associare ad ogni punto del piano uno ed un solo punto del piano stesso con in più la possibilità di tornare indietro in modo univoco da ogni punto di arrivo al suo punto di partenza.
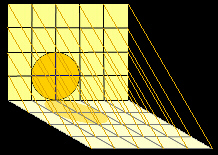
Nell'esempio dell'ombra vediamo che (figura a lato) i raggi del sole, che possono essere considerati paralleli, creano una corrispondenza biunivoca fra i punti della finestra ed i punti della sua ombra, cioè ad ogni punto della finestra corrisponde uno ed un solo punto della sua ombra e viceversa (per chiarezza abbiamo disegnato soltanto alcune frecce di corrispondenza), ma la corrispondenza avviene fra piani diversi.

L'impostazione esplicita di questo modo di osservare le figure studiandone le proprietà che restano invariate quando su di esse si opera con un gruppo di trasformazioni è dovuta a Felix Klein (1849 - 1925) che, nel 1872, tenne a tal proposito un ciclo di lezioni ad Erlangen (Programma di Erlangen).