|
PREMESSA. Scriviamo i sistemi di equazioni senza fare uso
della parentesi graffa.
Partiamo dall'equazione dell'affinità (con
ae - bd
≠ 0):
x'= ax+by+c
y'= dx+ey+f
|
La trasformazione dipende dai 6 parametri a, b, c, d, e, f;
x e y rappresentano rispettivamente l'ascissa e l'ordinata del punto di partenza, mentre x' e y' rappresentano quelle del punto trasformato.
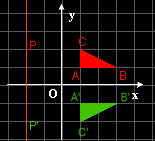
TERZO CASO x'= x
y'= -y
(a=1; b=c=0; d=0; e=-1; f=0).
Le ascisse restano uguali, mentre le ordinate cambiano segno: si tratta di
una simmetria rispetto all'asse delle x.
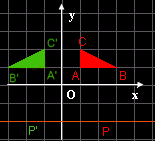
QUART O CASO
x'= -x
y'= y
(a=-1; b=c=0; d=0; e=1; f=0). Le
ascisse cambiano segno, mentre le ordinate restano uguali: si tratta di una simmetria rispetto all'asse delle y.
ESEMPIO
|
 |
 |
In entrambi i casi l'asse di simmetria è retta di punti uniti (cioè ogni punto dell'asse corrisponde a se stesso) e anche le rette perpendicolari agli assi sono unite, ma i loro punti no: ognuno di essi si trasforma nel suo simmetrico appartenente alla semiretta opposta. Inoltre prendiamo due punti A, B ed i loro simmetrici A', B': i segmenti AB ed A'B' sono congruenti, quindi la simmetria assiale è un'isometria,
cioè una trasformazione che fa corrispondere ad ogni coppia di punti una coppia
di punti che hanno la stessa distanza.
|
Simmetria rispetto all'asse x |
Simmetria rispetto all'asse y |
|
Notiamo che di tratta di un' isometria inversa, che cioè ribalta le figure e che, applicata due volte di seguito, dà luogo all'identità: si tratta di una trasformazione involutoria.
| |
|
| |