
Introduzione
Che
cosa sono i frattali?
Come
si realizzano i frattali?
Area
Download
CARATTERISTICHE
Autosimilarità
Perimetro
infinito e area finita
Dimensione
non intera
Struttura
complessa a tutte le scale di riproduzione
Dinamica
caotica
PERSONAGGI
Niels
Fabian Helge von Koch
Waclaw
Sierpinski
Gaston
Maurice Julia
Benoit
Mandelbrot
TIPI DI FRATTALI
Curva
di von Kock
Triangolo
di Sierpinski
Tappeto
di Sierpinski
Insieme
di Mandelbrot
Insiemi
di Julia
Frattali
di Newton
Drago
frattale
Cattedrale
frattale
Icebergs frattali
Alberi frattali
Curva logistica
Nuvole frattali
FRATTALI E REALTA'
...fisiologia
umana
...arte
...musica
...altri
campi
Bibliografia
e indirizzi utili
DIMENSIONE DEL TRIANGOLO DI SIERPINSKI
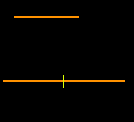 | |
Prendiamo ora un rettangolo e raddoppiamo la lunghezza di entrambe le sue dimensioni. Otteniamo quattro copie dell'originale. 4=22 |
 |
Se triplichiamo la lunghezza di entrambe le sue dimensioni otteniamo invece nove copie dell'originale. 9=32 |
 |
Prendiamo un cubo e raddoppiamo la lunghezza del suo lato. Otteniamo così otto copie dell'originale. 8=23 Se quadruplicassimo la lunghezza del lato, otterremmo ben sessantaquattro copie dell'originale! 64=43 |
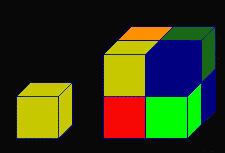 |
Organizziamo le nostre informazioni in una tabella.
| Figure | Dimensione | No. di copie |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
In generale, se n è il numero di ingrandimenti lineari, il numero di copie è rappresentato da una potenza di base n e di esponente la dimensione.
Sulla base di queste premesse calcoliamo la dimensione del triangolo di Sierpinski.
 |
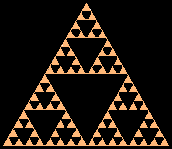 |
Raddoppiamo dunque il lato di un triangolo di Sierpinski: ci si aspetterebbe di ottenere quattro copie dell'originale, invece esse sono soltanto tre. (Ricordiamoci di non contare i buchi!)
Impostiamo dunque l'equazione 3 = 2d dove d è la dimensione.
Ora, poiché 21 = 2, e 22 = 4, il nostro numero deve essere compreso fra 1 e 2.
Ecco in evidenza il paradosso apparente dei frattali: sono più di una linea ma meno di una superficie.
Se sai risolvere un'equazione esponenziale, otterrai facilmente che
d =log3 2 = log3/log2 = 1,5849625....
Altrimenti, potrai arrivare a questo valore per successive approssimazioni secondo il procedimento che segue.
2 1.5 = 2.828427...
2 1.7 = 3.249009...
2 1.58 = 2.989698...
2 1.585 = 3.000077...
...
2 1.5849625 = 2.9999999...
2 1.5849626 = 3.0000002...
...