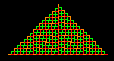
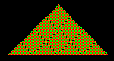
FRATTALE DI CESARO
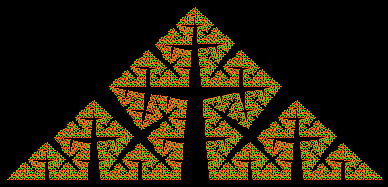
Si tratta di una generalizzaione della curva di von Koch, con angolo compreso fra 60° e 90°.
COSTRUZIONE
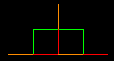
Si parte da un segmento AE, e si sostituisce ad esso la spezzata ABCDE costruita come in figura:
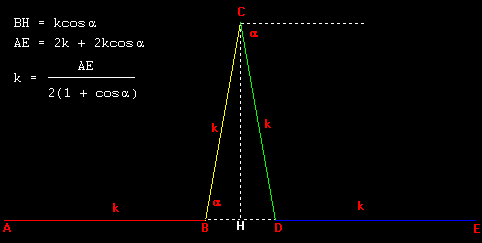
- Ogni segmento che compone la spezzata ha la stessa lunghezza k;
- 60° ≤ α ≤ 90°.
Ripetendo il procedimento su ogni segmento ottenuto si ottiene il frattale di Cesaro.
Nel caso particolare di α = 60° si ottiene la curva di von Koch.
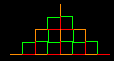
Cliccare su Successivo per visualizzare i primi quattro passi della costruzione del frattale di Cesaro nel caso di α = 72°;
per tornare indietro cliccate su Precedente.

Precedente Successivo
DIMENSIONE
La dimensione del frattale di Cesaro non è fissa, visto che dipende dall'angolo α. Ogni volta otteniamo 4 copie del segmento precedente, ognuna di misura 1/
Applicando la formula d =logn[f(n)]
= log[f(n)]/logn, presentata su dimensione non intera - seconda parte, abbiamo che:
- f(n) = 4 , infatti 4 sono le copie del segmento di base ad ogni passaggio;
- n = 2(1+cosα), infatti ogni segmento ha lunghezza 1/[2(1+cosα)] del precedente.
Vediamo alcuni casi particolari (le soluzioni sono data con 5 cifre significative):
| α = 60° | → | d = ln(4)/ln(1 + 2cos60°) = ln(4)/ln(3) = 1.26186
| α = 72° | → | d=ln(4)/ln(1 + 2cos 72°) = ln(4)/ln(2.61803) = 1.44042
| α = 85° | → | d=ln(4)/ln(1 + 2cos 85°) = ln(4)/ln(2.17431) = 1.78482
| α = 90° | → | d=ln(4)/ln(1 + 2cos 90°) = ln(4)/ln(2) = 2
| | | |
Nel caso di α = 90°, la dimensione non risulta frazionaria, pertanto il frattale rientra nelle "Curve di Peano"
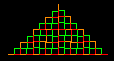
Come si vede dalle immagini in basso, dopo i primi 6 passi la curva tende a riempire un triangolo rettangolo isoscele.
APPROFONDIMENTO DI MATEMATICA E PROGRAMMA
©2010 www.webfract.it