Con questo metodo simuliamo le estrazioni del superenalotto, dalla prima alla sesta; quando ci interessa, simuliamo anche l'estrazione del jolly.
In questo modo scopriamo che
Schematizziamo la prima estrazione attraverso un diagramma ad albero (Figura 1) nel quale abbiamo denotato con
Lungo i rami dell'albero abbiamo riportato le relative probabilità

|
|
Schematizziamo anche la seconda estrazione attraverso un diagramma ad albero (Figura 2).
Sui rami terminali dell'albero abbiamo denotato con VV l'evento "vengono estratti due dei numeri giocati", con VF l'evento "il primo numero numero estratto è uno dei numeri giocati e il secondo no", con FV l'evento "il primo numero numero estratto non è uno dei numeri giocati e il secondo sì", con FF l'evento " nessuno dei due numeri estratti è uno dei numeri giocati".
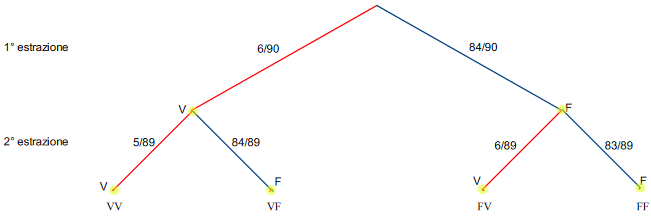
Le probabilità alla seconda estrazione dipendono dalla prima, infatti, dopo ogni estrazione, vengono modificati sia il numero dei casi possibili (che diminuiscono ogni volta di 1), sia quello dei casi favorevoli, che variano a seconda di quello che è successo nell'estrazione precedente. Abbiamo 4 casi:
Riferiamoci alla figura 3: nella rappresentazione ad albero abbiamo evidenziato il percorso che ci interessa.
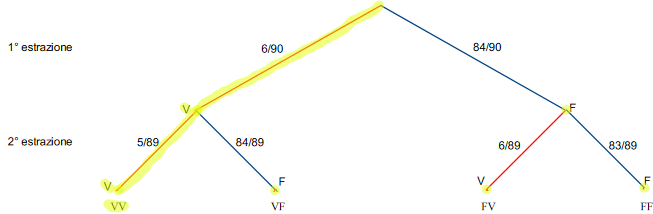
Indicando con E2 l'evento "nelle prime due estrazioni vengono estratti due dei numeri giocati ", vediamo che esso è un evento composto il cui verificarsi è dato dall'intersezione degli eventi
Scriviamo
p(E2) = p(V ∩ V) = (6/90) × (5/89)
Così facendo applichiamo direttamente il teorema delle probabilità composte:
siano A e B due eventi casuali compatibili e dipendenti. Allorap(A ∩ B) = p(A) • p(B|A) = p(B) • p(A|B)
La probabilità che si verifichino contemporaneamente due eventi è data dal prodotto della probabilità che si verifichi il primo moltiplicata per la probabilità che si verifichi il secondo condizionato al verificarsi del primo, come pure dalla probabilità che si verifichi il secondo moltiplicata per la probabilità che si verifichi il primo condizionato al verificarsi del secondo.
|
|
Osservando la tabella dei valori di probabilità si nota che gli eventi scritti con lo stesso colore sono equiprobabili. Riassumiamo il tutto
| V | Casi | Probabilità |
|---|---|---|
| 2 | 1 | (6×5)/(90×89) |
| 1 | 2 | 2(6×84)/(90×89) |
| 0 | 1 | (84×83)/(90×89) |
I dati possono anche essere organizzati secondo il seguente schema, che ci sarà molto utile in seguito.
| Estrazioni | Indovinati | Casi |
|---|---|---|
| 1° | 1 0 | 1 1 |
| 2° | 2 1 0 | 1 2 1 |
Nella seconda estrazione possiamo indovinare entrambi i numeri, oppure 1 solo numero, o, infine nessun numero: abbiamo scritto 2 1 0.
Possiamo indovinare entrambi i numeri in un solo caso (che dopo il primo V otteniamo ancora V), 1 solo numero in 2 casi (che dopo il primo V otteniamo F oppure che dopo il primo F otteniamo V) e, infine, nessun numero in 1 caso (che dopo il primo F otteniamo ancora F); abbiamo scritto 1 2 1.
prime due estrazioni
Noterete che la seconda riga si ottiene dalla prima disponendo 1 agli estremi e sommando la coppia di termini della riga superiore.
Si parla delle configurazioni semplici e si verifica la la probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
Calcolatore online della probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
per calcolare la probabilità di vincita al superenalotto con l'aiuto del calcolo combinatorio.
Calcolare la probabilità di vincita al superenalotto con tutti i passaggi per ogni caso.
©
www.webfract.it
- Questo sito è di esclusiva proprietà degli autori, Eliana Argenti e Tommaso Bientinesi.
Ne è vietata la riproduzione e la copia senza la preventiva autorizzazione scritta di webfract.it
Approfondimento su termini di utilizzo