Applicheremo la definizione classica di probabilità, faremo poi uso del calcolo combinatorio e del teorema delle
probabilità composte.
Chi lo preferisce può trovare la dimostrazione eseguita passo per passo.
Indichiamo con Quindi p(E6) indica la probabilità di fare 6 al superenalotto con 1 giocata e così via.
E6 l'evento "fare 6 al superenalotto con 1 giocata"
E5+1 l'evento "fare 5 +1 al superenalotto con 1 giocata"
...
E2 l'evento "fare ambo al superenalotto con 1 giocata"
Calcoliamole, notando che:
Con questa premessa possiamo dire che il numero di casi ugualmente possibili è dato dalle combinazioni di 90 oggetti presi a 6 a 6 , che indichiamo con C90,6C90,6 = 90! / (6! × 84!) = 622˙614˙630
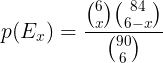
per x ∈ {6, 4, 3, 2}
dove x indica quanti numeri sono stati indovinati.
Dimostrazione
Del denominatore abbiamo già detto; nel numeratore dobbiamo inserire i casi a noi favorevoli. Dei numeri giocati
x devono appartenere all'insieme dei 6 numeri estratti, 2≤ x ≤ 6: in tutto C6,x
I restanti, cioè 6-x, devono appartenere all'insieme degli 84 numeri non estratti: in tutto C84,6-x
I due eventi devono verificarsi contemporaneamente, dunque, applicando il teorema delle probabilità composte, moltiplichiamo i valori trovati.
Calcoliamo p(E6)
Visto che dobbiamo indovinare 6 dei 6 numeri estratti, mentre non indovinarne 0, i casi favorevoli corrispondono a C6,6 × C84,0 = 1 × 1 = 1
Concludiamo che
p(E6) = 1/622˙614˙630
Calcoliamo p(E4)
Visto che dobbiamo indovinare 4 dei 6 numeri estratti, mentre non indovinarne 2, i casi favorevoli corrispondono a C6,4 × C84,2 =15 × 3˙486 = 52˙290Concludiamo che
p(E4) = 52˙290/622˙614˙630 ≈ 1/11˙907
Calcoliamo p(E3)
Visto che dobbiamo indovinare 3 dei 6 numeri estratti, mentre non indovinarne 3, i casi favorevoli corrispondono a C6,3 × C84,3 = 20 × 95˙284 = 1˙905˙680Concludiamo che
p(E3) = 1˙905˙680/622˙614˙630 ≈ 1/327
Calcoliamo p(E2)
Visto che dobbiamo indovinare 2 dei 6 numeri estratti, mentre non indovinarne 4, i casi favorevoli corrispondono a C6,2 × C84,4 = 15 × 1˙929˙501 = 28˙942˙515Concludiamo che
p(E2) = 28˙942˙515/622˙614˙630 ≈ 1/22
Si parla delle configurazioni semplici e si verifica la la probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
Calcolatore online della probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
Come calcolare la probabilità di vincita al superenalotto se non si conosce il calcolo combinatorio.
©
www.webfract.it
- Questo sito è di esclusiva proprietà degli autori, Eliana Argenti e Tommaso Bientinesi.
Ne è vietata la riproduzione e la copia senza la preventiva autorizzazione scritta di webfract.it
Approfondimento su termini di utilizzo