MATEMATICA CON JAVASCRIPT

CALCOLO COMBINATORIO ONLINE
1 - Configurazioni semplici

Configurazioni con ripetizione

DISPOSIZIONI SEMPLICI E FUNZIONI INIETTIVE

D_n,k è anche il numero di funzioni iniettive da un insieme di k elementi ad uno di n elementi.
Infatti in questo caso:
Il primo elemento può essere scelto
in n modi diversi;
il secondo elemento può essere scelto
in n - 1 modi diversi;
il terzo elemento può essere scelto
in n - 2 modi diversi;
. . . . .
il k-esimo elemento può essere scelto
in n -k + 1 modi diversi.

PERMUTAZIONI SEMPLICI E ORDINAMENTO

P_n esprime il numero di ordinamenti possibili negli n elementi.

Discende immediatamente dal fatto che le permutazioni di un insieme di n elementi differiscono tra di loro per l’ordine.

PERMUTAZIONI SEMPLICI E BIEZIONI

P_n può anche esprimere il numero di biiezioni di un insieme di n elementi in un insieme di n elementi, oppure di un insieme di n elementi in sé.
Esempio: In quanti modi si possono sedere 4 persone su quattro sedie numerate da 1 a 4?
Uno dei modi è rappresentato nella figura in basso (two-line notation):

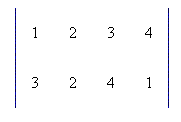
La scrittura soprastante esprime che la prima persona si è seduta nella sedia numero 3, la seconda in quella numero 2, ..., la quarta nella sedia numero 1
Possiamo anche scrivere:
f(1) = 3; f(2) = 2;
f(3) = 4; f(4) = 1

E' chiaro poi che la prima persona potrà sedersi in 4 modi diversi, la seconda in 3 modi diversi, la terza in 2 modi diversi e infine l'ultima in 1 solo modo. In tutto abbiamo 4 × 3 × 2 × 1 = 4! = 24 modi diversi.

Un bell'esempio che lega i due concetti

In quanti modi diversi posso contare gli oggetti posti sulla mia scrivania?

E' chiaro che per contare gli oggetti abbiamo bisogno di procedere con un certo ordine e di associare ogni oggetto alla successione dei naturali, a partire da 1...

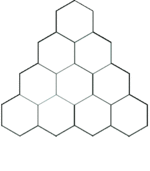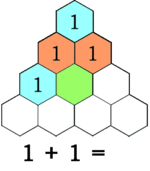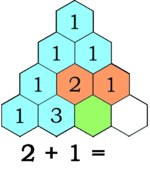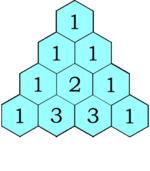
COMBINAZIONI SEMPLICI E TRIANGOLO DI TARTAGLIA

Si costruisce in modo tale che i numeri siano ricavati dalla somma dei due numeri adiacenti della riga superiore

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

Gli elementi del triangolo di Tartaglia sono detti coefficienti binomiali poiché coincidono con i coefficienti delle potenze di un binomio.
Ad esempio
(a+b)⁰ = 1
(a+b)¹ = a + b
(a+b)² = a² + 2ab + b²

Ogni elemento del triangolo si può individuare per mezzo del numero di riga e del numero di posto. Ora, analizzando la quinta riga (ricordiamo che si parte da zero) 1 5 10 10 5 1, scopriamo facilmente che una cinquina è composta da:

 5 numeri estratti = C_5,1
10 ambi = C_5,2
10 terni = C_5,3
 5 quaterne = C_5,4
 1 cinquina = C_5,5

Blaise Pascal, nel 1654, scrisse un intero libro, Le Triangle Aritmétique, dedicato a questo triangolo e alle sue proprietà, in particolare nel campo del calcolo combinatorio. Uno studio importante che portò a ribattezzare il celebre triangolo con il nome di "Triangolo di Pascal". Come tale esso è ormai noto in tutto il mondo.

APPROFONDIMENTO su Progetto Polimath

Si dicono disposizioni semplici di n oggetti distinti di classe k, con k <= n, tutti i gruppi che si possono formare con k degli n oggetti, considerando distinti i gruppi che differiscono per almeno un elemento o per l'ordine.
Il loro numero si indica con D_n,k. Risulta:

D_n,k = n(n-1)...(n-k+1) = n!/(n - k)!

Si ammette, per convenzione, che 0! = 1. In questo modo la formula precedente ha sempre significato.

1. Conta l’ordine;
2. non sono ammesse ripetizioni.

IN EVIDENZA DAL SITO

CALCOLATRICE
SCIENTIFICA


CON SPIEGAZIONI
ED ESEMPI

TARTAMONDO - PER BAMBINI

AREA GIOCHI

COMBINAZIONI VINCENTI

NUMERI PER IL SUPERENALOTTO

Verifica le probabilità di vincita al superenalotto che abbiamo dato ricordando che la probabilità di fare:

1. 6 =
   
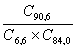
2. 5 + 1 =
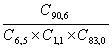