A
rgomenti correlati:
TRASFORMAZIONI IN MATEMATICA
Vettori
Dato un segmento AB possiamo orientarlo in due modi diversi, fissando o il verso di percorrenza da A verso B, oppure da B verso A.
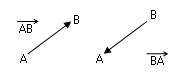
Fra i segmenti orientati si definisce la relazione di equipollenza: due segmenti orientati si definiscono equipollenti quando hanno la stessa lunghezza, la stessa direzione e lo stesso verso.
Tale relazione è di equivalenza, in quanto gode delle proprietà riflessiva, simmetrica e transitiva. L’equipollenza suddivide perciò i segmenti orientati del piano in classi di equivalenza. Ogni classe è chiamata vettore e contiene tutti e soli i segmenti fra loro equipollenti.
Traslazione
Fissato nel piano un vettore, una traslazione è una trasformazione geometrica che a ogni punto P fa corrispondere il punto P' tale che PP' è equipollente a v (su PP' e v dovrebbe esserci la freccia). Si scrive 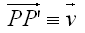 Osservate l'immagine in basso: 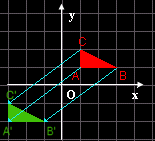
Ogni segmento AB ed il suo corrispondente A'B' sono non solo congruenti (si tratta di un'isometria) ma anche paralleli ed ugualmente orientati; inoltre nella traslazione anche tutti i segmenti che congiungono punti corrispondenti (come AA', BB', CC') sono equipollenti, cioè hanno la stessa direzione, la stessa lunghezza e lo stesso verso.
Le rette unite sono quelle che uniscono punti corrispondenti: ad esempio un punto della retta AA' si trasforma in un punto sempre appartenente alla stessa retta.
Infine, se le componenti della traslazione sono entrambe nulle, questa si trasforma in un'identità (tutti i punti sono uniti); altrimenti nessun punto è unito.
APPROFONDIMENTO
Dilatazioni - contrazioni
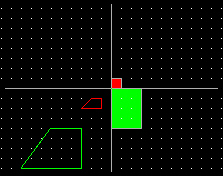
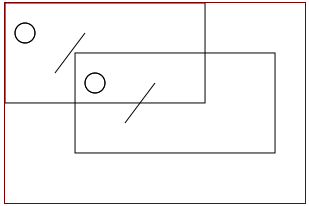
Nell'immagine in alto è rappresentata la trasformazione di base (quadrato rosso - rettangolo verde) ed una trasformazione di un trapezio rettangolo (rosso) in un altro trapezio rettangolo (verde).
Possiamo vedere che
rette parallele si trasformano in rette parallele; gli assi cartesiani e l'origine sono uniti; le distanze non si mantengono. L'equazione che rappresenta la trasformazione è 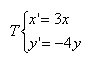
Se P e P' , Q e Q' sono coppie di punti corrispondenti, se
d(P,Q) < d(P',Q') si parla di contrazione, mentre se
d(P,Q) > d(P',Q') si parla di dilatazione.
APPROFONDIMENTO
|
Metodo translate()
Riposiziona l'origine (0,0) della canvas e tutti i disegni sono riferiti alla nuova origine.
SINTASSI
context.translate(x,y);
x = spostamento orizzontale in pixel
y = spostamento verticale in pixel
ESEMPIO DI CODICE (ctx.translate(70,50);)
Come si vede dall'esempio, una volta chiamato il metodo, tutte le coordinate vengono riferite alla nuova origine (70,50)

Il metodo scale() ci permette di dilatare o contrarre la canvas sia orizzontalmete che verticalmente. SINTASSI
context.scale(x,y);
x = dilatazione o contazione orizzontale: (1=100%, 0.5=50%, 2=200%, etc.)
y = dilatazione o contazione orizzontale: (1=100%, 0.5=50%, 2=200%, etc.)
Nell'immagine in alto la figura di partenza è il quadrato celeste, al quale sono state applicate due dilatazioni e una contrazione. Come si vede, varia anche lo spessore del contorno, cosa che non capita con le trasformazioni geometriche in matematica.
Scalare rispetto a un punto qualunque
Vi invitiamo, se volete provare il metodo scale() rispetto all'origine, a visionare la sezione
Precedente - Successivo
|
IN EVIDENZA DAL SITO 

CALCOLATRICE
SCIENTIFICA
CON SPIEGAZIONI
ED ESEMPI

TARTAMONDO - PER BAMBINI
AREA GIOCHI



Ti potrebbero anche interessare:
Traslare o scalare con il metodo transform()
|



