A
rgomenti correlati:
Coordinate omogenee
Chiamiamo coordinate omogenee di un punto P(x,y) del piano cartesiano qualsiasi terna omogenea (X,Y,Z) di numeri reali tali che
Z ≠ 0 e x = X/Z, y = Y/Z
Ad esempio, il punto A(5,4), ha coordinate omogenee (5,4,1) oppure (10,8,2) e così via.
Prodotto di matrici
Consideriamo il prodotto riga per colonne, indicato con il simbolo ⊗: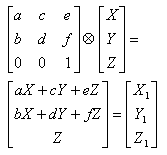 
Esso equivale alle equazioni in coordinate omogenee
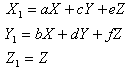
e, in coordinate non omogenee
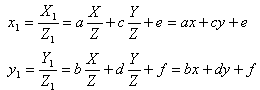
Di seguito, per semplicità, useremo coordinate del tipo (h,k,1).
Traslazione
context.transform(1,0,0,1,e,f), da cui si ottiene
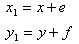
Il comando è equivalente a
context.translate(e,f)
Dilatazione rispetto all'origine degli assi cartesiani con fattori kx e ky
context.transform(kx,0,0,ky,0,0), infatti
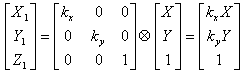
ovvero, in coordinate non omogenee
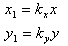
Il comando è equivalente a
context.scale(kx,ky)
Rotazione di centro l'origine degli assi cartesiani e angolo orientato α
context.transform(Math.cosα,Math.sinα,
-Math.sinα,Math.cosα,0,0), infatti
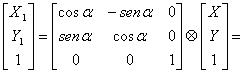
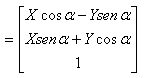
ovvero, in coordinate non omogenee
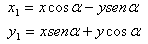
Il comando è equivalente a
context.rotate(α)
Ti potrebbero anche interessare:
Disegnare rettangoli
Funzioni di testo
Colori
Crea i tuoi colori
|
Premessa
Figura 1
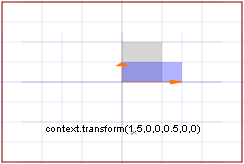
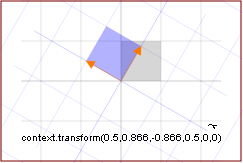
 Nella figura 1 vediamo il metodo transform() applicato a una canvas nella quale, dopo aver tracciato gli assi cartesiani (con il sistema di riferimento predefinito) e la griglia di base, avevamo inserito l'immagine a destra.
Come si vede dall'esempio, la trasformazione, di tipo lineare, ha riguardato l'intera canvas.
Il metodo, come sempre, è stato richiamato prima di disegnare.
SINTASSI
context.transform(a,b,c,d,e,f); 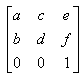 Viene applicata la matrice di trasformazione e dunque otteniamo
(x1 = ax +cy + e) and (y1 = bx +dy + f) Vediamo dunque che si tratta di un'affinità.
Attraverso il metodo sono realizzabili traslazioni, cambiamenti di scala e rotazioni, spiegate nella sezione Facciamo il punto, a sinistra nella pagina; se abbiamo l'equazione di un'affinità, ad esempio x1 = 0.75x + 0.5y - 1
y1 = 2x - 1.5y +3 potremo applicare il metodocontext.transform(0.75,0.5,2,1.5,- u,3*u); [u = unità di misura]
NOTA BENE Se volete riferirvi a un diverso sistema di riferimento dovrete operare una opportuna trasformazione.
Vediamo come varia il reticolato di base al variare dei singoli parametri.
- Parametro a: dilatazione o contrazione orizzontale
Codice:
context.transform(a,0,0,1,0,0);
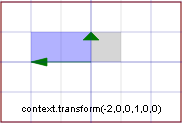
E' equivalente al codice context.scale(a,1); EsempioPonete a = -2
Risultato:
x1 = -2x
y1 = y
| 
|
Otteniamo una variazione di scala lungo l'asse x e di rapporto -2 |
Parametro b: inclinazione dell'asse orizzontale
Codice
context.transform(1,b,0,1,0,0); EsempioPonete b = +0.75
Risultato:
x1 = x
y1 = +0.75x + y [Tenete conto del sistema di riferimento]
| 
|
L'ascissa resta invariata mentre l'ordinata varia linearmente in funzione dell'ascissa
|
- Parametro c: inclinazione dell'asse verticale
Codice
context.transform(1,0,c,1,0,0);
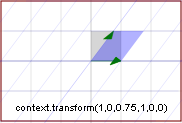
EsempioPonete c = -1.25
Risultato:
x1 = x + 1.25y
y1 = y [Tenete conto del sistema di riferimento]
| 
|
L'ordinata resta invariata mentre l'ascissa varia linearmente in funzione dell'ordinata
|
- Parametro d: dilatazione o contrazione verticale
Codice
context.transform(1,1,0,d,0,0);
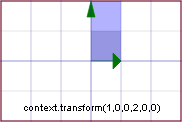
E' equivalente al codice context.scale(1,d); Esempio Ponete d = 2
Risultato:
x1 = x
y1 = 2y
Risultato:
| 
|
Variazione di scala lungo l'asse y di rapporto 2 |
- Parametri e,f.
Provocano una traslazione rispettivamente orizzontale e verticale
Precedente - - Successivo
|
IN EVIDENZA DAL SITO Clicca sull'immagine per accedere al tutorial dinamico sul metodo transform()!
Potrai provare trasformazioni predefinite o crearne di tue proprie! 
CALCOLATRICE
SCIENTIFICA
CON SPIEGAZIONI
ED ESEMPI
TARTAMONDO - PER BAMBINI
AREA GIOCHI
Clicca sull'immagine per accedere al tutorial dinamico sul metodo transform()!
Potrai provare trasformazioni predefinite o crearne di tue proprie!
|
Passione per i viaggi e la natura