MATEMATICA CON JAVASCRIPT

CHIOCCIOLA DI PASCAL (LIMAÇON)

PAGINE 1 - 2 - 3 - 4 - 5 - 6

CURVE DI EQUAZIONE POLARE ρ = a + bcos(kα)

Fissiamo nel piano una circonferenza di centro C e raggio r.
Fissiamo sulla circonferenza un punto O.
Per ogni punto A appartente alla circonferenza prendiamo i due punti P ed R che si trovino sulla semiretta OA e a distanza k da A.

La lumaca di Pascal può essere definita come il luogo geometrico dei punti P ed R al variare di A sulla circonferenza (anzi, per essere esatti, basta che A vari in una delle due semicirconferenze in cui la circonferenza è divisa dal diametro OD).

Riferiamoci alla FIGURA 1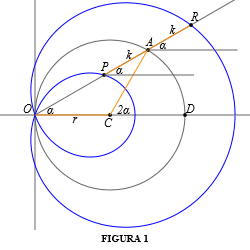

Indichiamo con α l'angolo AÔC. Considerato che il triangolo AOC è isoscele, possiamo ottenere facilmente le coordinate del punto A:

A_x = r + cos2α
A_y = sin2α

Il punto R ha coordinate

R_x = A_x + kcosα = r + cos2α + kcosα = (k + 2rcosα)cosα
R_y = A_y + ksinα = sin2α + ksinα = (k + 2rcosα)sinα

Dunque possiamo esprimere la chiocciola con l'equazione polare ρ = k + 2rcosα; 0 ≤ α < 2π

[per i passaggi cfr. la dimostrazione di pagina 2]

La forma della curva varia a seconda della relazione che esiste fra il diametro della circonferenza 2r e la distanza fissata k.

In analogia con quanto fatto con il primo caso trattato, distingueremo i casi k < 2r, k = 2r, k > 2r.

Il tuo browser non supporta the "canvas" tag

←  PAGINE 1 - 2 - 3 - 4 - 5 - 6   →

IN EVIDENZA DAL SITO

CALCOLATRICE
SCIENTIFICA


CON SPIEGAZIONI
ED ESEMPI

TARTAMONDO - PER BAMBINI

AREA GIOCHI