Sia E3 l'evento "fare 3 al superenalotto con 1 giocata". Dimostriamo che p(E3) ≈ 1/327
Se preferisci, puoi anche calcolare tale probabilità attraverso il calcolo combinatorio. o con l'aiuto dei diagrammi ad albero.
L'evento E3 = "fare terno al superenalotto con 1 giocata" si verifica quando abbiamo indovinato solo 3 dei 6 numeri estratti.
Denotiamo con
e consideriamo innanzitutto l'intersezione degli eventi V∩V∩V∩F∩F∩F, ognuno dei quali è condizionato al verificarsi dei precedenti; abbreviamo tale intersezione con VVVFFF
Seguiamo la tabella.
| Estrazione | Casi favorevoli | Casi possibili | Probabilità |
|---|---|---|---|
1° | 6 | 90 | 6/90 |
6 dei 90 numeri ci sono favorevoli | |||
2° | 5 | 89 | 5/89 |
I nostri numeri vincenti sono ormai 5; quelli rimasti nell'urna sono 89 | |||
3° | 4 | 88 | 4/88 |
I nostri numeri vincenti sono ormai 4; quelli rimasti nell'urna sono 88 | |||
4° | 84 | 87 | 84/87 |
i numeri diversi dai nostri sono 84; quelli da estrarre sono 87 | |||
5° | 83 | 86 | 83/86 |
i numeri diversi dai nostri sono 83; quelli da estrarre sono 86 | |||
6° | 82 | 85 | 82/85 |
i numeri diversi dai nostri sono 82; quelli da estrarre sono 85 | |||
Applicando il teorema delle probabilità composte (cfr Probabilità di vincere al superenalotto con una giocata), otteniamo
p(VVVFFF) = (6/90)×(5/89)×(4/88)×(84/87)×(83/86)×(82/85)
La tabella riporta il caso in cui si immagini di si immagini di indovinare solo i primi 3 numeri, che abbiamo indicato con V,V,V,F,F,F; d'altra parte, potremmo fare terno in 20 modi diversi, tutti equiprobabili (si tratta di tutti i possibili terni distinti che si possono formare con 6 elementi). Elenchiamo i casi.
| 1 | V,V,V,F,F,F | 6 | V,F,V,F,V,F | 11 | F,V,V,V,F,F | 16 | F,V,F,F,V,V |
|---|---|---|---|---|---|---|---|
| 2 | V,V,F,V,F,F | 7 | V,F,V,F,F,V | 12 | F,V,V,F,V,F | 17 | F,F,V,V,V,F |
| 3 | V,V,F,F,V,F | 8 | V,F,F,V,V,F | 13 | F,V,V,F,F,V | 18 | F,F,V,V,F,V |
| 4 | V,V,F,F,F,V | 9 | V,F,F,V,F,V | 14 | F,V,F,V,V,F | 19 | FF,F,V,F,V,V |
| 5 | V,F,V,V,F,F | 10 | V,F,F,F,V,V | 15 | F,V,F,V,F,V | 20 | F,F,F,V,V,V |
Applichiamo il teorema delle probabilità totali (cfr Probabilità di vincere al superenalotto con una giocata). Otteniamo che la probabilità di fare terno al superenalotto è
p(E3) = 20p(V,V,V,F,F,F)
cioè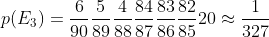
Si parla delle configurazioni semplici e si verifica la la probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
Calcolatore online della probabilità di vincita al superenalotto con l'aiuto delle combinazioni semplici.
per calcolare la probabilità di vincita al superenalotto con l'aiuto del calcolo combinatorio.
Calcolare la probabilità di vincita al superenalotto con l'aiuto dei diagrammi ad albero.
©
www.webfract.it
- Questo sito è di esclusiva proprietà degli autori, Eliana Argenti e Tommaso Bientinesi.
Ne è vietata la riproduzione e la copia senza la preventiva autorizzazione scritta di webfract.it
Approfondimento su termini di utilizzo