rose a n petali quinto caso - matematica con HTML5 canvas e JavaScript su webfract

SIANO k ∈ Z₀; a < b; a ≥ 0

In questo caso abbiamo due insiemi di petali, entrambi in numero di k, che si dispongono in questo modo:

se k è dispari, i petali di dimensione inferiore, inscritti nella circonferenza di raggio (b - a), sono interni a quelli di dimensione maggiore, inscritti nella circonferenza di raggio (b + a);
se k è pari, i petali di dimensione inferiore, inscritti nella circonferenza di raggio (b - a), sono alternati a quelli di dimensione maggiore, inscritti nella circonferenza di raggio (b + a).

Ricordiamo inoltre che, per quanto riguarda i seguenti casi:

a = 0
Abbiamo pubblicato il capitolo delle curve rodonee
(a ≠ 0) ∧ (k = 1)
Abbiamo pubblicato il capitolo limaçon di Pascal; in particolare, per k = 1, a = 1, b = 2, guardate "una chiocciola particolare"

ESEMPI DI SVILUPPO DELLE CURVE

PRIMO ESEMPIO

Le curve, rispettivamente di equazione polare

f: ρ = 2 + 5cos(3φ),
g: ρ₁ = cos(3φ)

sono state disegnate con colori diversi a intervalli di π/3.

Ogni π/3, |ρ₁| = 1, dunque ρ₁ oscilla fra 1 e -1,
invece ρ oscilla fra 7 e -3.

Mentre la curva g si sviluppa completamente quando φ = π, la f si sviluppa completamente quando φ = 2π; inoltre mentre la curva g ha 3 petali, la f ne ha 6, dei quali i tre di dimensione maggiore sono inscritti nella circonferenza di raggio 7, mentre i tre di dimensione minore sono inscritti nella circonferenza di raggio 3.

SECONDO ESEMPIO

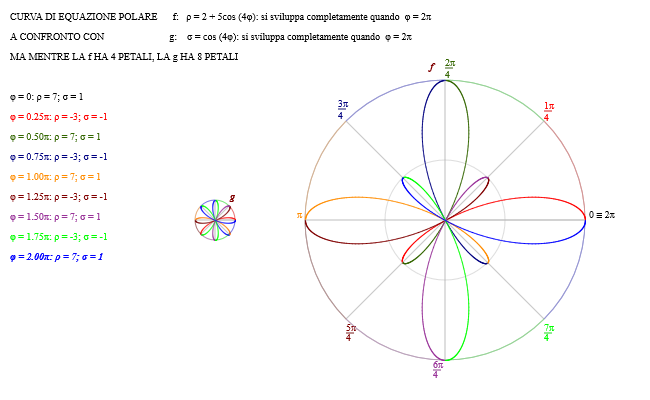Le curve, rispettivamente di equazione polare

f: ρ = 2 + 5cos(4φ),
g: ρ₁ = cos(4φ)

sono state disegnate con colori diversi a intervalli di π/4.

Ogni π/4, |ρ₁| = 1, dunque ρ₁ oscilla fra 1 e -1,
invece ρ oscilla fra 7 e -3.

Entrambe le curve si sviluppano completamente quando φ = 2π, e hanno 8 petali; nel caso della f vediamo che i quattro petali di dimensione maggiore sono inscritti nella circonferenza di raggio 7, mentre i quattro di dimensione minore sono inscritti nella circonferenza di raggio 3.

← PAGINE 1 - 2 - 3 - 4 →

IN EVIDENZA DAL SITO