|
SECONDA COSTRUZIONE
 Clic sull'immagine per vedere i passi successivi. In questo esempio costruiamo la curva di equazione ρ = cos(4φ), e quindi di equazione parametrica (x = cos(4φ)cosφ) and (y = cos(4φ)senφ), ogni π/4. Ogni π/4 ρ ha modulo 1 - infatti risulta |cos(4φ)| = 1 per 4φ = hπ, h intero -
In particolare: -
ρ = - 1 per φ = π/4
- ρ = + 1 per φ = π/2
- ρ = - 1 per φ = 3/4π
- ρ = + 1 per φ = π
- ρ = - 1 per φ = 5/4π
- ρ = + 1 per φ = 3/2π
- ρ = - 1 per φ = 7/4π
- ρ = + 1 per φ = 2π: solo adesso il secondo estremo della curva è di nuovo in (1,0) e questa si chiude. [Infatti (x = cos2π = 1) and (y = sen2π = 0)]
Riassumendo, le condizioni per cui la curva ρ = cos(kφ) si chiude sono due:-
[kφ = (2h+1)π] and [φ= (2c-1)π] con c intero positivo. (Caso di chiusura con φ = π e ρ = -1)
- OPPURE
[kφ =2hπ] and [φ=2cπ], sempre con c intero positivo. (Caso di chiusura con φ = 2π e ρ = 1)
Di questi due casi dobbiamo trovare il più piccolo c intero positivo tale che h sia intero, e se i due valori di c coincidono dobbiamo prendere il caso in cui la φ risultante é minore. Nel primo caso h = kc - (k+1)/2, nel secondo caso h = kc.
Ovviamente, questo secondo valore è maggiore del primo.
Se k è dispari, k+1 è pari, dunque h è intero ∀ c, nelle condizioni poste.
Scegliendo c = 1 otteniamo φ = π. Se per esempio n=3, in entrambi i casi h é intero per c = 1, ma il minore φ possibile si ha nel primo caso (φ = (2*c-1)π).
La seconda soluzione é anche valida, e φ = 2π, ma al secondo giro la curva viene ricalcata.
Visto che si forma un petalo ogni π/k, il numero di petali è k quando k è dispari, e 2k quando k è pari.
- k sia un numero razionale = n/d: allora, se il prodotto nd è dispari, la curva si chiude a un angolo di πd, mentre, se nd è pari, la curva si chiude a un angolo di 2πd.
DUE ESEMPI
  Clic sulle immagini per vedere i passi successivi. Nel primo esempio osserviamo la curva di equazione ρ = cos(5/3φ) ogni 3/5π
Dopo 3π la curva si chiude formando 5 petali. Nel secondo esempio osserviamo la curva di equazione ρ = cos(2/3φ) ogni 3/2π
Dopo 6π la curva si chiuse formando 4 petali. Visto che si forma un petalo ogni πd/n, il numero di petali è n quando nd è dispari, e 2n quando nd è pari. - k sia un numero irrazionale: allora la curva ha infiniti petali, non è chiusa ed è densa rispetto a un qualsiasi punto del cerchio circoscritto.
ESEMPI
  
  
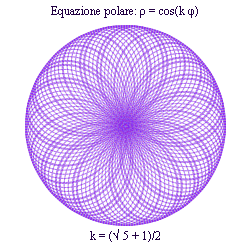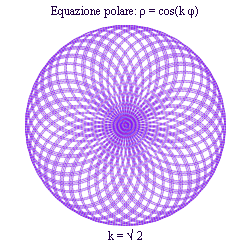
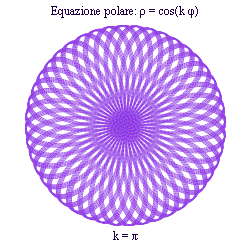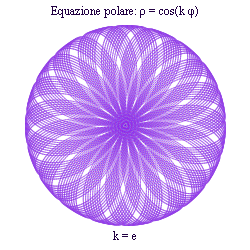
← PAGINE 1 - 2 - 3 - 4 →
|
IN EVIDENZA DAL SITO 
CALCOLATRICE
SCIENTIFICA
CON SPIEGAZIONI
ED ESEMPI
TARTAMONDO - PER BAMBINI
AREA GIOCHI
|
La passione per i viaggi e la natura nel nuovo sito di Tommaso Bientinesi