MATEMATICA CON JAVASCRIPT
CHIOCCIOLA DI PASCAL (LIMAÇON)

MATEMATICA CON JAVASCRIPTCHIOCCIOLA DI PASCAL (LIMAÇON) |
 |
|
UNA CHIOCCIOLA PARTICOLARE
Si tratta della chiocciola di equazione polare ρ = k(1 + 2cosα), che è anche la più nota. Questa curva risolve il problema della trisezione dell'angolo (vedi figura in alto a destra): si voglia trisecare l'angolo ∠RQP, individuato dall’asse di simmetria OR della chiocciola e dalla semiretta di origine Q che interseca la curva in P. Si congiunge P con O. L'angolo ∠QPO risolve il problema. Segue la dimostrazione nella quale, per semplicità, abbiamo scelto k = 1.
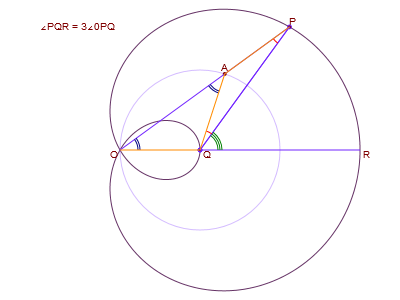 DIMOSTRAZIONE
CHIOCCIOLA DI PASCAL COME INVILUPPO DI CIRCONFERENZE
La chiocciola di Pascal può essere definita come l'inviluppo di circonferenze che passano per un punto P fissato (noi abbiamo scelto l'origine degli assi cartesiani) e che hanno centro appartenente a una data circonferenza. Il punto P può avere distanza dal centro della circonferenza maggiore, uguale, o minore del raggio. L' animazione proposta di seguito permette di osservare il formarsi della traccia durante il rotolamento: dopo aver scelto la posizione del punto, cliccate sul pulsante "ANIMA" ANIMAZIONEAbbiamo fissato una circonferenza γ e un punto P (nelle figure in basso il punto è interno al cerchio) Abbiamo costruito le circonferenze che abbiano centro su γ e passino per P.
|
IN EVIDENZA DAL SITO
CALCOLATRICE
TARTAMONDO - PER BAMBINI
AREA GIOCHI

|
CURVE DI EQUAZIONE POLARE ρ = a + bcos(kα): Sommario
Matematica con javascript, area Canvas: Indice
Matematica con javascript Indice
©2002 - 2014 www.webfract.it