MATEMATICA CON JAVASCRIPT

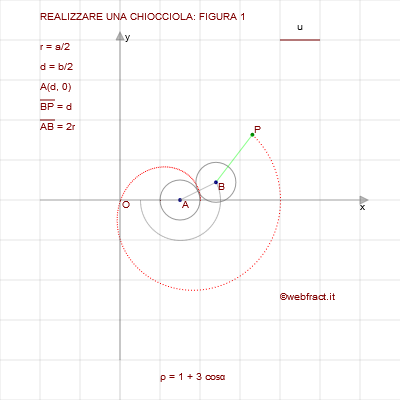Vogliamo costruire la chiocciola di equazione ρ = a + bcosα con il metodo indicato a pagina 1

Riferiamoci alla figura a sinistra (FIGURA 1).

I due cerchi, c₁ e c₂, di centri rispettivamente A e B, hanno lo stesso raggio r = a/2.

Il cerchio c₁ è fisso, mentre c₂ rotola senza strisciare intorno a c₁.

Al cerchio c₂ è fissato un punto P, a distanza d da B uguale a b/2: il punto P descrive la chiocciola quando il cerchio c₂ rotola e la sua posizione, ad ogni istante t, dipende dall'arco α descritto da B, centro di c₂.

Il centro di c₁ è A(d,0).

Dimostriamo che si ottiene l'equazione parametrica

x(t) = (a + bcost)cost
y(t) = (a + bcost)sent

e, quindi, l'equazione polare ρ = a + bcosα

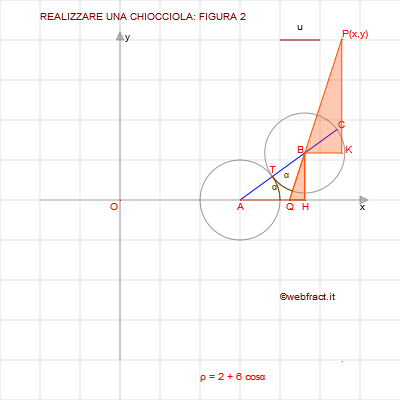Riferiamoci alla FIGURA 2

Calcoliamo la posizione di P dopo che il cerchio rotante ha percorso l'arco α.

Per trovare l'ascissa del punto P, calcoliamo la misura di OA + AH + BK

(1)    x = d + 2rcosα + dcos(2α)

[Il triangolo ABH è rettangolo; i triangoli BPK e QBH sono simili; l'angolo HQB è esterno al triangolo AQB e quindi è congruente alla somma degli angoli non adiacenti, entrambi di ampiezza α (in radianti).]

Per trovare l'ordinata del punto P, calcoliamo la misura di HB + KP

y = 2rsenα + dsen(2α)

Ricordando che cos2α = 2cos²α -1 e che sen2α = 2senαcosα, si ottiene:

(2)    [x(α) = (2 r + 2 d cosα)cosα]   and   [y(α) = (2 r + 2dcosα)senα]
e, infine, sapendo che a = 2r, che b = 2d, e ponendo α = t:

x(t) = (a + bcost)cost
y(t) = (a + bcost)sent

www.tommasobientinesi.it