|
 
Se vogliamo ottenere la silhouette di una cardioide ci possiamo servire di un recipiente di forma cilindrica che abbia le pareti riflettenti e cambiarne gradualmente l'inclinazione rispetto ai raggi di luce incidenti.
Quando il fondo viene illuminato solo per riflessione sulle pareti interne del recipiente, si
vede una curva luminosa, detta caustica di riflessione, o catacaustica, causata dalla concentrazione della luce in quella regione.
Nell'immagine a sinistra si vede la foto di una vecchia tazza piena d'acqua, ripresa al mattino, illuminata dai raggi del sole; in quella a destra, invece, vediamo un cappuccino, in un recipiente metallico, illuminato da una lampada.
Quando la sorgente di luce è all'esterno del cilindro, come si vedrà, la caustica diventa rapidamente equivalente a quella generata da una luce a distanza infinita.
La maggior parte degli oggetti riflette una parte della luce che li colpisce ed è possibile verificare, quando la superficie è levigata, la legge di riflessione della luce: il raggio incidente, il raggio riflesso e la normale alla superficie riflettente nel punto di incidenza giacciono tutti sullo stesso piano e l’angolo di riflessione è uguale all’angolo di incidenza.
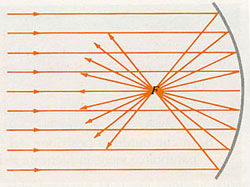  Nel caso di una superficie parabolica i raggi riflessi si concentrano in un punto, il fuoco, e intorno ad esso si concentra una grande quantità di energia capace, in determinate condizioni, di fondere, o addirittura incendiare, un oggetto.
Le altre curve non hanno in generale questa proprietà e i raggi riflessi si concentrano non in un punto, ma su una curva: la caustica
Il nome deriva dal latino causticus (greco καυστóς - kaustós - bruciato, combustibile) e dunque la sua etimologia richiama quella del fuoco, ad esempio, di una parabola.
(Le immagini a sinistra sono tratte da science storming)
Scegli il tipo desiderato quindi clicca sul pulsante per avviare l'animazione.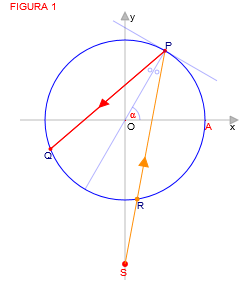 
L'idea per simulare la caustica è stata la seguente.
Abbiamo fissato una circonferenza γ di raggio unitario e di centro l'origine.
Indicato con SP il generico raggio incidente, e con R il punto in cui esso interseca la circonferenza, si ha che il raggio riflesso PQ è il simmetrico della corda PR rispetto al raggio OP.
Detto α l'angolo ∠AOP, per trovare tutti i punti P è bastato far variare α fra 0 e 2π nel caso in cui S appartenga alla circonferenza, fra 0 e π nel caso in cui S sia esterna alla circonferenza, infatti solo in questo caso i raggi si possono riflettere.
[dal sito www.geometryexpressions.com] | 
FIGURA 2
|
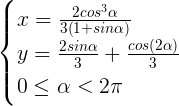
Permette di trovare, al variare di α, l'angolo, espresso in radianti, che il raggio OP forma con il semiasse delle x positive (vedi FIGURA 1), tutti i punti appartenenti al contorno della caustica.
Se tracciamo i segmenti (cosα, sinα) (x, y) otteniamo la curva riportata in FIGURA 2. Questo è il caso in cui si immagina che la sorgente luminosa sia posta sulla circonferenza. |
← PAGINE 1 - 2 - 3 - 4 →
|
IN EVIDENZA DAL SITO 
CALCOLATRICE
SCIENTIFICA
CON SPIEGAZIONI
ED ESEMPI
TARTAMONDO - PER BAMBINI
AREA GIOCHI
|
La passione per i viaggi e la natura nel nuovo sito di Tommaso Bientinesi