MATEMATICA CON JAVASCRIPT
CARDIOIDE

MATEMATICA CON JAVASCRIPTCARDIOIDE |
 |
|
|
Si ottiene per a = ± b e k = 1, dunque ha equazione polare ρ = a(1 ± cosα), a meno di rotazioni. Il nome, derivante dal greco καρδιοειδήϛ (kardioeidès), cuoriforme, fu attribuito alla curva da Johann Castillon (Castiglione del Valdarno, 11 gennaio 1704 – Berlino, 11 ottobre 1791), matematico italiano, il cui vero nome era Giovanni Francesco Salvemini, in un articolo pubblicato da Philosophical Transactions della Royal Society nel 1741. Si tratta dunque di una curva a forma di cuore - anche la matematica ha un cuore? - 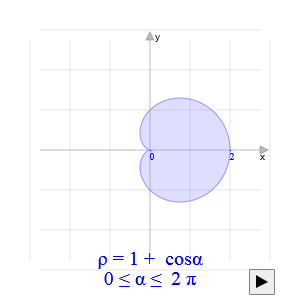 Clic sull'immagine per vedere altre cardioidi. Come potete vedere scorrendo le immagini, la cardioide può essere ottenuta, a meno di una rotazione rispetto all'origine degli assi, come grafico di varie equazioni polari, ad esempio: Visto che sia il seno che il coseno di un angolo sono compresi fra -1 e 1, tutte le cardioidi sono tangenti internamente alla circonferenza di centro l'origine e raggio = 2a. Se |a| = |b| > 1, variano solo le dimensioni della curva, pertanto basterà considerare il caso COME COSTRUIRE UNA CARDIOIDEPRIMO METODO: COME EPICICLOIDE Si definisce epicicloide, composto di epi (su) e cicloide, la curva generata da un punto di una circonferenza che rotola sulla superficie esterna di un'altra circonferenza: è un caso particolare dell' epitrocoide, dal greco επι (epi, "su") e τροχοιδήϛ (trocoidès: a forma di ruota), curva generata da un punto di una figura che rotola su di un'altra. Come si vede dall'animazione, la cardioide può essere definita come il percorso di un punto fissato sulla circonferenza di un cerchio di raggio r che sta rotolando senza strisciare intorno a un altro cerchio sempre di raggio r. Scegliendo il sistema di riferimento in modo che il cerchio fisso abbia centro nel punto (r,0), si ottiene l'equazione parametrica (1) [ x(α) = r(1 + 2cosα + cos2α)] and y(α) = r(1 + 2senα + sen2α)] Ricordando che cos2α = 2cos2α -1 e che sen2α = 2senαcosα, si ottiene: [x(α) = 2r(1 + cosα)cosα] and [y(α) = 2r(1 + cosα)senα] x(t) = a(1 + cost)cost L'equazione cartesiana della cardioide è
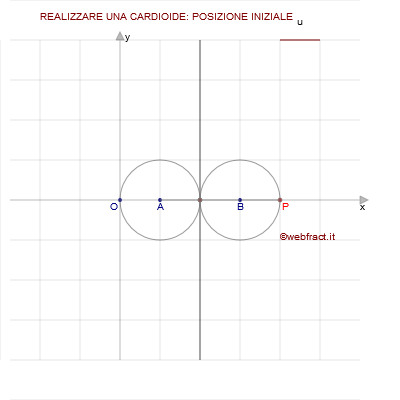  Posizione iniziale: Riferisciti alla FIGURA 2 Calcoliamo la posizione di P dopo che il cerchio rotante ha percorso l'arco α. Per trovare l'ascissa del punto P, calcoliamo la misura di
OA + AH + BK Per trovare l'ordinata del punto P, calcoliamo la misura di
HB + KP Se il raggio è uguale a r, si ottiene, ovviamente, l'equazione (1)
|
IN EVIDENZA DAL SITO
CALCOLATRICE
TARTAMONDO - PER BAMBINI
AREA GIOCHI

|
Ci serviremo delle equazioni parametriche (1) da cui ricaviamo, innanzitutto, che y/x = tgα
Ricordiamo che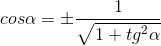
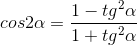
Sostituiamo questi valori nella prima delle due equazioni. Ricaviamo
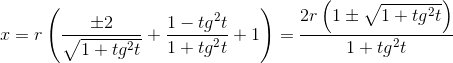
Sostituiamo a tgα y/x. Ricaviamo:
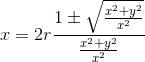
Svolgiamo i calcoli e isoliamo il radicale:

Eleviamo al quadrato per eliminare il doppio segno, ed ecco l'equazione cartesiana della cardioide
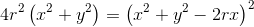
CURVE DI EQUAZIONE POLARE ρ = a + bcos(kα): Sommario
Matematica con javascript, area Canvas: Indice
Matematica con javascript Indice
©2002 - 2014 www.webfract.it