Introduzione alle equazioni e curve parametriche

Contatti	MATEMATICA CON JAVASCRIPT EQUAZIONI E CURVE PARAMETRICHE - INTRODUZIONE

F
acciamo il punto.
Argomenti correlati:

Equazioni parametriche

Una curva in un piano è detta parametrizzata se l'insieme delle coordinate (x,y) dei punti della curva sono funzioni della variabile t:
x= f(t) and y = g(t), t ∈ D, dove D è un insieme di numeri reali.
La variabile t è detta parametro e le relazioni fra x, y e t sono dette equazioni parametriche.

Notare che la rappresentazione parametrica non è unica, infatti il parametro si può scegliere in modi diversi; di solito si cerca di sceglierlo nel modo più adatto a semplificare i calcoli.

Esempio di una possibile rappresentazione parametrica della circonferenza:

Svolgendo i calcoli si trova infatti

x ² + y² = 1

Prova online

Il programma ha lo stesso tipo di funzionamento di quello relativo di...

Equazioni parametriche della circonferenza di centro C(x₀,y₀)

Osserviamo la figura. Fissato sulla circonferenza il raggio CB parallelo all'asse delle x e ad esso equiverso, abbiamo che,
∀ P appartenente alla circonferenza, il raggio CP risulta equipollente al vettore OP'. P', come abbiamo visto, ha coordinate (cos(AÔP'), sen(AÔP')).
Le coordinate del generico punto P sono pertanto

Portando a primo membro x₀ e y₀ ed elevando al quadrato, otteniamo:
(x - x₀)² + (y - y₀)² = 1

Prova online

Equazioni parametriche di una ellisse

Se applichiamo la dilatazione di equazioni (a > 0 e b > 0)

all'equazione parametrica della circonferenza unitaria, otteniamo l'equazione parametrica dell'ellisse in forma canonica:

CONVERSIONE IN EQUAZIONE CARTESIANA

Eleviamo al quadrato primo e secondo membro delle due equazioni e dividiamo, rispettivamente, la prima equazione per a² e la seconda per b². Otteniamo: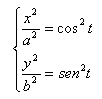

E quindi, commando membro a membro,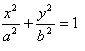

Che è l'equazione canonica dell'ellisse di semiassi a e b.

Prova online

EQUAZIONE PARAMETRICA DELLA CIRCONFERENZA UNITARIA

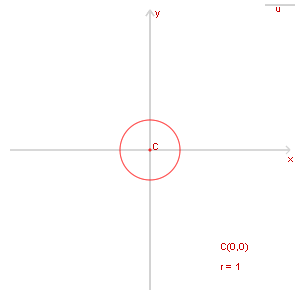Sia data una circonferenza di raggio unitario e centro C≡O(0,0) (detta anche circonferenza unitaria).

Possiamo scrivere la sua equazione cartesiana tenendo conto del fatto che la circonferenza in questione è il luogo geometrico dei punti che hanno dal punto C distanza uguale al raggio. Scriveremo dunque:

x ² + y² = 1

Sappiamo che la circonferenza che ha centro nell'origine e raggio = 1 è anche detta circonferenza goniometrica unitaria qualora su di essa sia fissato un verso di percorrenza potitivo (per convenzione, il verso antiorario): fissato il punto A(1,0) come origine degli archi, avremo che un suo punto P determina, insieme al punto A, l'arco orientato AÔP.

Indicando con α la misura dell'arco orientato AÔP, e sotto le ipotesi poste, si definiscono, rispettivamente:

cosα = Ascissa di P;
senα = Ordinata di P.

0 ≤ α < 2π
-1 ≤ cosα ≤ 1
-1 ≤ senα ≤ 1
cos²α + sen²α = 1

FATTE QUESTE PREMESSE

Esprimiamo la circonferenza unitaria mediante le seguenti equazioni parametriche, usando t al posto di α, in quanto, di solito, è questo il nome che viene dato al parametro: