Premettiamo le seguenti definizioni:
- Diciamo sezione aurea di un segmento la parte del segmento che è media proporzionale fra l'intero segmento e la parte rimanente.
- Indichiamo con φ il rapporto fra la sezione aurea di un segmento e il segmento stesso.
- Diciamo rapporto aureo, che indichiamo con Φ, il rapporto fra l'intero segmento e la sua sezione aurea.
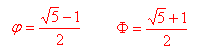
Come calcolare φ e Φ è riportato nella sezione Facciamo il punto, in basso nella pagina.
In questa pagina, dopo aver presentato la costruzione geometrica della sezione aurea di un segmento e quella di un segmento di cui è data la sezione aurea, spiegheremo come rappresentare su un schermo grafico un rettangolo aureo.
COSTRUZIONE GEOMETRICA DELLA SEZIONE AUREA DI UN SEGMENTO
|
|
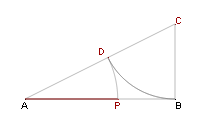
Cliccate sul pulsante: - INIZIA per osservare la costruzione passo per passo.
- DIMOSTRAZIONE per visualizzare la dimostrazione.
- AGGIORNA per cancellare tutto e ricominciare da zero.
|
|
COSTRUZIONE GEOMETRICA DI UN SEGMENTO DATA LA SUA SEZIONE AUREA
|
|
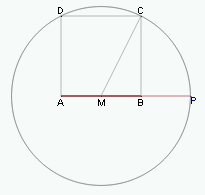
Cliccate sul pulsante: - INIZIA per osservare la costruzione passo per passo.
- DIMOSTRAZIONE per visualizzare la dimostrazione.
- AGGIORNA per cancellare tutto e ricominciare da zero.
|
|
COSTRUZIONE GEOMETRICA DI UN RETTANGOLO AUREO
Si tratta di un rettangolo in cui il rapporto fra il lato maggiore e il minore è Φ.
|
| |
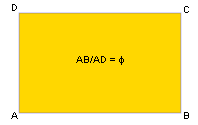
Cliccate sul pulsante: - INIZIA per osservare la costruzione passo per passo.
- ANIMATO per osservare la costruzione in automatico.
- AGGIORNA per cancellare tutto e ricominciare da zero.
|
|
RAPPRESENTARE UN RETTANGOLO AUREO SU UNO SCHERMO GRAFICO
La costruzione mediante canvas e javascript è molto semplice: vi spieghiamo come farlo attraverso un apposito tutorial. Vi invitiamo, se volete provare il vostro codice, a visionare la sezione PROVA TU - CREA UN RETTANGOLO AUREO
Successivo: proprietà del numero aureo
|
IN EVIDENZA DAL SITO 
CALCOLATRICE
SCIENTIFICA
CON SPIEGAZIONI
ED ESEMPI

TARTAMONDO - PER BAMBINI
AREA GIOCHI



INDICE SEZIONE AUREA
[1] - Costruzione geometrica della sezione aurea di un segmento
[2] - Costruzione geometrica di un segmento data la sua sezione aurea
[3] - Costruzione geometrica di un rettangolo aureo
[4] - Rappresentare un rettangolo aureo su uno schermo grafico
[5] - Proprieta' del numero aureo e piano cartesiano
[6] - Proprieta' fondamentale del rettangolo aureo
[7] - Introdurre un procedimento iterativo
[8] - Approssimazione del rettangolo aureo mediante una sequenza di quadrati
[9] - Provare la costruzione passo per passo o animata
[10] - Costruire il nautilus
[11] - Il modo più semplice per costruire il nautilus con riga e compasso
|
F
acciamo il punto.
Argomenti correlati:
Come calcolare la sezione aurea di un segmento
Se indichiamo con l la lunghezza del segmento, e con x la lunghezza della sua sezione aurea, possiamo scrivere la proporzione
l : x = x : (l-x)Visto che in una proporzione il prodotto dei medi è uguale a quello degli estremi, ricaviamo che x2 = l2 - lx ⇒ x2 + lx - l2 = 0 Si tratta di risolvere un'equazione di secondo grado che ha Δ = l√5 Visto che x deve essere positivo, la soluzione che accettiamo è x = l(√5 - 1)/2 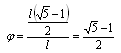 [Indichiamo con φ il rapporto fra la sezione aurea e l'intero segmento. Esso è un numero irrazionale. φ ≈ 0.6180340.]
Come calcolare il rapporto aureo
Il rapporto aureo che, come abbiamo detto, indica il rapporto fra l'intero segmento e la sua sezione aurea, è la costante
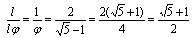 La costante, universalmente nota come Φ, dall'iniziale del nome dello scultore greco Fidia, La costante, universalmente nota come Φ, dall'iniziale del nome dello scultore greco Fidia, Φ =(√5 +1)/2 ≈ 1.6180340
è la soluzione positiva dell'equazione

TORNA SU
Link utili
Math.it - Geometria con Cabri: sezione aurea.
La sezione aurea nell'architettura - Sapienza - Università di Roma
Appunti che sono l’elaborazione dei testi presentati in bibliografia e per uso interno alla Facoltà di Architettura Valle Giulia,
nell’ambito del corso di Teorie e tecniche costruttive nel loro sviluppo storico del prof. Giorgio Monti

DAL NOSTRO SITO
Cosa si nasconde dietro la croce dei templari?
(la sezione aurea) - Due tipi di croce templare costruiti passo per passo
|


