ALBERI DI PITAGORA COSTRUITI CON METODO GEOMETRICO PASSO PER PASSO - INTRODUZIONE

Figura 1	Figura 2	Figura 3	Figura 4

Il nome di questi alberi frattali deriva dal fatto che essi sono alberi binari in cui la dimensione di ogni nodo genitore (a) è collegata a quella dei due figli, sinistro (c) e destro (b), dal teorema di Pitagora: a² = b² + c².
L'idea tridimensionale che danno gli alberi è dovuta al fatto che i quadrati sono stati riempiti con colori digradanti

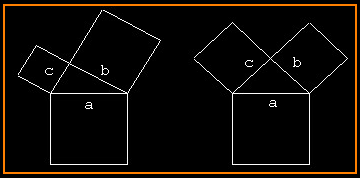
Ogni quadrato ha un lato in comune con un triangolo rettangolo, che a sua volta ha gli altri due lati in comune con altri due quadrati e così via.
Per comodità indicheremo ogni triangolo rettangolo mediante il suo angolo acuto minore, e in particolare:

nella figura 1 i triangoli rettangoli hanno gli angoli acuti di 30° e 60°, e gli angoli si dispongono sempre nello stesso verso. Li indicheremo con P₃₀;

nella figura 2 i triangoli rettangoli sono isosceli. Li indicheremo con P₄₅;

nella figura 3 i triangoli rettangoli hanno gli angoli acuti di 30° e 60°, ma gli angoli si dispongono secondo un verso alternato.
Tale immagine è detta anche albero di Natale [cfr. library.thinkquest.org]. Per distinguerli dai triangoli P₃₀ li indicheremo con N₃₀

Nella figura 4 i triangoli rettangoli hanno gli angoli acuti di 30° e 60°, e gli angoli si dispongono in verso casuale: come vedremo si formano figure diverse e molto simpatiche, tanto che li potremmo soprannominare alberi matti. Li indicheremo con C₃₀

1. visto che ogni quadrato, in ogni passaggio, genera due quadrati, il numero di quadrati aggiunti al passaggio n è 2ⁿ;
2. Ad ogni passaggio il perimetro aumenta; in particolare:
   • nel caso degli alberi del tipo delle figure 1, 3 e 4 esso aumenta del fattore 1/2 + (√3)/2.
     Il triangolo rettangolo con gli angoli acuti di 30° e 60° è infatti la metà di un triangolo equilatero che ha lato uguale a quello del quadrato di partenza;
   • nella figura 2 esso aumenta del fattore 2/√2 = √2.
     Il triangolo rettangolo con gli angoli acuti di 45° è infatti la metà di un quadrato che ha la diagonale uguale al lato del quadrato di partenza.
   
   Gli alberi di Pitagora hanno pertanto perimetro infinito
3. Per il teorema di Pitagora la somma delle aree dei quadrati aggiunti in ogni passaggio è uguale a quella del quadrato di partenza, che per comodità possiamo porre uguale a 1.
   L'area sembra dunque diventare infinita, quando il numero di passaggi tende a infinito; in effetti invece già a partire dal quinto passaggio la figura piega su se stessa, rimanendo racchiusa in una superficie limitata.
   Gli alberi di Pitagora hanno pertanto perimetro infinito e area limitata.
4. La struttura che osserviamo in scala normale viene ripetuta infinite volte all'interno della scala più piccola, e la possiamo ritrovare qualsiasi sia la potenza della lente d'ingrandimento che usiamo: essi sono pertanto autosimili.
5. Gli infiniti vertici degli alberi di Pitagora, quando la lunghezza dei lati tende a zero, sono tutti punti angolosi, per cui non si riesce a trovare alcuna zona "regolare" che ammetta tangente. [cfr. Problema delle tangenti alle curve frattali]

Alberi di Pitagora: Introduzione      Pit₄₅   Pit₃₀   Codice   Di Natale   Casuali    Generalizzati   Di Natale generalizzati