Metodo rotate() - matematica con JavaScript

Contatti	MATEMATICA CON JAVASCRIPT - GUIDA CANVAS 11 - Trasformazioni geometriche: rotate() Precedente - Indice guida canvas - Successivo

A
rgomenti correlati:

TRASFORMAZIONI IN MATEMATICA

Rotazione

Per stabilire una rotazione occorre fissare un punto O, centro della rotazione, ed un angolo orientato ß che è positivo se la rotazione è in verso antiorario, negativo altrimenti.
Ad ogni punto P del piano distinto da O si fa corrispondere il punto P' tale che:
OP = OP';
l'angolo PÔP' = ß
Il punto O, centro della rotazione, corrisponde a se stesso.

Figura 1
Centro O ed angolo di -60°

Figura 2
Centro O ed angolo di +60°

Nella figura 2 è stato messo in evidenza il fatto che la rotazione è un'isometria: i segmenti corrispondenti hanno la stessa lunghezza.

APPROFONDIMENTO

Simpatiche applicazioni

FRAMMENTO DI CODICE

   const u =60;
  const O1x=c.width/2;   //ascissa origine
  const O1y=c.height/2;  //ordinata origine
  ctx.translate(O1x,O1y);
  var colori = new Array("rgba(255,255,0,0.5)",
  "rgba(0,255,255,0.5)","rgba(255,0,255,0.5)",
  "rgba(0,180,180,0.5)","rgba(180,180,0,0.5)",
  "rgba(180,0,0,0.5)","rgba(0,180,0,0.5)",
  "rgba(0,0,255,0.5)")
 
  for (i=0; i<8; i++){
    ctx.rotate(-Math.PI/6);
    ctx.fillStyle=colori[i]
    ctx.fillRect(0,0,u,-u)
   }

RUOTARE I CARATTERI DI UNA SCRITTA

FRAMMENTO DI CODICE

  const u =48;
  const O1x=c.width/2;   //ascissa origine
  const O1y=c.height/2 + 5;  //ordinata origine
  ctx.translate(O1x,O1y);
  var scrivi = new Array("M","a", "k", "e",
   "\u2764","L","o", "v", "e","\u2764","N",  
   "o", "t","\u2764","W","a", "r","\u2763",
   "\u2763","\u2763","")
  var colori = new Array("rgba(0,0,180,0.75)",
  "rgba(102,153,255,0.75)","rgba(153,0,102,0.75)",
  "rgba(51,102,51,0.75)","rgba(255,255,0,0.75)",
  "rgba(255,102,0,0.75)","rgba(255,0,0,0.75)")
  for (i=0; i<18; i++){
    ctx.rotate(Math.PI/9);
    ctx.beginPath();
    ctx.fillStyle=colori[i%7]
    ctx.fillText(scrivi[i],u,-u)
    ctx.strokeText(scrivi[i],u,-u)
   }

Come si vede dall'esempio, con il metodo rotate() è possibile ruotare non solo i punti, ma anche i caratteri.
Nell'esempio abbiamo disposto i caratteri in forma circolare memorizzandoli in un array e facendoli scrivere uno dopo l'altro dopo aver ruotato ogni volta di π/9 (= 2π/18): la scritta infatti è di 18 caratteri.

Ti potrebbero anche interessare:
Ruotare con il metodo transform()
Disegnare rettangoli
Funzioni di testo
Colori
Crea i tuoi colori

Metodo rotate()

Ruota il disegno corrente dell'angolo dichiarato. A differenza che in matematica, il verso di rotazione positivo è quello orario.

SINTASSI

context.rotate(angolo);

angolo = angolo di rotazione espresso in radianti

ESEMPIO DI CODICE ctx.rotate(60*Math.PI/180): ruota di 60° in verso orario intorno all'origine degli assi, cioè intorno al vertice della canvas in alto a sinistra.

NOTA BENE - Occorre usare il metodo prima di disegnare.

Ruotare intorno all'origine degli assi cartesiani scelta a piacere

Supponiamo di aver creato un sistema di riferimento cartesiano ortogonale con l'origine O(Ox,Oy).
Vogliamo ruotare un quadrato intorno a O di un angolo β in senso antiorario. Come procedere?

PASSO 1

Operate la traslazione di vettore (Ox,Oy): context.translate(Ox,Oy);

PASSO 2

Operate la rotazione: context.rotate(- angolo);

PASSO 3

Disegnate il quadrato.

Nella figura a sinistra, nella quale abbiamo riportato anche gli assi cartesiani, il quadrato di partenza è stato disegnato in rosso, quello di arrivo in azzurro.
Visto che l'angolo di rotazione positivo, nel metodo rotate(), è quello orario, se vogliamo ruotare in verso antiorario dobbiamo inserire un angolo negativo.
NOTA BENE
E' essenziale rispettare l'ordine delle trasformazioni

Ruotare intorno a un punto qualunque: esempio

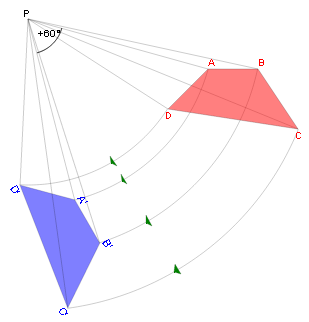
Nell'immagine vediamo il quadrato di vertici A(0,0) B(1,0) C(1,1) D(0,1) che è stato ruotato di +45° (in senso antiorario) intorno al punto P(2.-3).

Fare clic sul pulsante "INIZIA" per eseguire la costruzione passo per passo (1 clic per ogni passo); fare in alternativa clic sul pulsante "COMPLETO" per eseguire la costruzione completa; il pulsante "AGGIORNA", infine, cancella tutto e si riparte da zero.

Ruotare intorno a un punto qualunque P(x₀, y₀)

PASSO 1

Operate la traslazione di vettore (x₀, y₀): context.translate(x₀, -y₀);

PASSO 2

Operate la rotazione di angolo β e centro O(0,0): context.rotate(-β);
Se β è espresso in gradi, trasformatelo in radianti mediante la regola: β_rad = β° × π /180

PASSO 3

Operate la traslazione inversa, di vettore (-x₀, -y₀): context.translate(-x₀, y₀);

Precedente - Successivo

IN EVIDENZA DAL SITO

Clicca sull'immagine per accedere al tutorial dinamico sul metodo rotate()!
Potrai cambiare ascissa e ordinata del centro di rotazione, il quadrato di partenza, l'angolo di rotazione.