MATEMATICA CON JAVASCRIPT

IL MODO PIU' SEMPLICE PER COSTRUIRE IL NAUTILUS CON RIGA E COMPASSO

[1] - [2] - [3] - [4] - [5] - [6] - [7] - [8] - [9] - [10] - [11]

Dovrete partire da un rettangolo aureo. (Costruzione)

Seguite poi i seguenti passi:

Tracciate un arco, come riportato in figura, nel quadrato APQD.	Tracciate le diagonali DB e CP che si incontrano nel punto O
Da R = [QP] ∩ [DB], tracciate il segmento [RS] // [AB]	Trovate ora il punto di incontro di [RS] con [PC] e quindi la parallela a BC

CONTINUIAMO CON LA COSTRUZIONE PASSO PER PASSO O ANIMATA (PER 11 PASSI)

NOTA BENE - Il programma fa uso del tag HTML5 canvas e javascript. Gli utenti MSIE possono visualizzare la canvas solo dalla versione 9 in poi.

Costruzione passo per passo	Cliccate sul pulsante: INIZIA per osservare la costruzione passo per passo. ANIMATO per osservare la costruzione in automatico. Per interrompere l'animazione premere STOP AGGIORNA per cancellare tutto e ricominciare da zero.
Your browser does not support the HTML5 canvas tag.

PERCHE' SI PUO' FARE COSI'?

I rettangoli aurei ABCD e QPBC sono simili. [proprietà fondamentale del rettangolo aureo]

Tracciamo le diagonali DB e CP dei due rettangoli, che si incontrano nel punto O: questo divide entrambe le diagonali in parti proporzionali a Φ.
Infatti DB ⊥ CP sono perpendicolari (guarda gli angoli), e i triangoli ABD, DCB, QPC, BCP, DOC e BOP sono simili per il primo criterio di similitudine dei triangoli. In particolare, possiamo scrivere:

DO : OB = DC : PB = CO : OP = CB : PB = Φ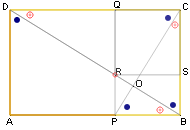

Sia R il punto d'incontro di QP con DB. Anche DQR e RSB sono triangoli simili ai precedenti, quindi R divide sia QP che DB in parti proporzionali a Φ. Dunque:

DR : RB = DQ : RS = CB : QR = Φ

Il segmento RS divide il rettangolo aureo PBCQ nel quadrato RSCQ e nel nuovo rettangolo aureo RSBP.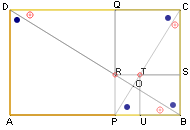

Sia T il punto d'incontro di RS con la diagonale CP. Anche T divide in parti proporzionali a Φ sia la diagonale che il segmento RS. (Basta ripetere il ragionamento precedente considerando i triangoli CBP e CST.)

Dunque otteniamo nuovamente la suddivisione di un rettangolo aureo in un quadrato e un rettangolo aureo.

Ripetendo il procedimento avremo una successione di rettangoli aurei e quadrati, che converge al punto O.

[1] - [2] - [3] - [4] - [5] - [6] - [7] - [8] - [9] - [10] - [11]

IN EVIDENZA DAL SITO

CALCOLATRICE
SCIENTIFICA


CON SPIEGAZIONI
ED ESEMPI

TARTAMONDO - PER BAMBINI

AREA GIOCHI

[1] Φ

Simbolo usato per il rapporto aureo: Φ =(√5 +1)/2 ≈ 1.6180340

[2] Triangoli simili

Due triangoli sono simili se hanno tutti gli angoli uguali e i lati corrispondenti in proporzione

[3] Primo criterio di similitudine

Se due triangoli hanno due angoli uguali, allora sono simili.

TORNA SU