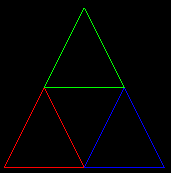
Frattali di Sierpinski

IL TRIANGOLO DI SIERPINSKI CON IL  METODO DI BARNSLEY

Il metodo utilizzato nell'animazione costruisce un frattale come collage di copie ridotte ed opportunamente trasformate di un oggetto iniziale (nell'esempio la scritta FRATTALE).
Si parte in questo caso dal frattale già formato e se ne osservano le peculiarità. Nell'esempio del triangolo di Sierpinski si nota che esso è composto da tre triangoli, ognuno di lato metà di quello di partenza, disposti, tanto per fissare le idee, uno in basso a sinistra, uno in basso a destra, uno in alto.
Lo stesso schema peraltro si ripete su ognuno dei tre triangoli sopra menzionati: possiamo allora immaginare la figura finale come sequenze di:

da applicare su ognuna delle scritte che man mano si formano.
Nell'animazione abbiamo attuato solo quattro cicli, ma già si intuisce l'immagine che si formerà: la scritta, sempre più piccola, tenderà a diventare un punto e i punti si disporranno secondo lo schema tipico del triangolo di Sierpinski. L'immagine finale perciò non dipende dalla scritta iniziale ma solo dal procedimento costruttivo.
Il problema che si pone riguarda il numero delle scritte, che ogni volta triplica, e che rende la costruzione realizzabile praticamente solo per pochi passi.
E' qui che è interviene la straordinaria idea di Michael E. Barnsley, che egli chiamò "il gioco del caos".
Si predispone un'urna con tre palline, una rossa, una verde e una blu; ogni pallina contiene le istruzioni per una trasformazione.

Pallina rossaContrazione di un mezzo
Spostamento in basso a sinistra di lunghezza fissa 1/2 		triangolo attuale possibili trasformazioni
Pallina verdeContrazione di un mezzo
Spostamento in alto di lunghezza fissa 1/2
Pallina bluContrazione di un mezzo
Spostamento in basso a destra di lunghezza fissa 1/2

Dopo aver fissato nel piano un punto iniziale arbitrario P0, si estrae a caso una pallina e si esegue la corrispondente trasformazione ottenendo il punto P1. La pallina viene reinserita nell'urna, si procede ad una nuova estrazione e si applica la trasformazione a P1 ottenendo P2. Ripetendo il procedimento un elevato numero di volte (anche svariate migliaia), i punti tendono a disporsi secondo la forma desiderata, nel nostro caso il triangolo di Sierpinski.

E' questa, sicuramente, una importante novità. I metodi analizzati precedentemente sfruttavano l'applicazione ciclica di processi costruttivi abbastanza intuitivi: ad esempio il triangolo di Sierpinski si otteneva "asportando" successivamente parti del triangolo di partenza, mentre nel fiocco di Koch si "aggiungevano" di volta in volta triangolini. Il metodo L-System prevede la trasformazione ad ogni passo di tutti i lati già disegnati. Barnsley, invece, pensò di partire da un punto e spostarlo, scegliendo a caso tra le trasformazioni di base, in successive posizioni che, quasi per magia, si rivelano appartenenti al frattale finale. Il metodo da lui sviluppato prende il nome di IFS (Iterated Function System - sistema di funzioni iterate), ideato da John Hutchinson nel 1871.
Un particolare frattale IFS è dunque definito dalle regole usate per trovare, e disegnare, il punto successivo e  dalla probabilità di scegliere una particolare funzione fra quelle di base.  Il punto iniziale invece non ha effetto sulla forma finale.
E' proprio magia? Ovviamente no. Si tratta invece di una importante conseguenza dell'autosimilarità. Questo fatto costituisce però anche un limite, infatti il metodo di Barnsley è applicabile solo a frattali autosimili

PROVA IL PROGRAMMA CHE COSTRUISCE IL TRIANGOLO DI SIERPINSKI PASSO PER PASSO COL METODO DI BARNSLEY

     

Introduzione
 Sierpinski
Triangolo g.
Triangolo IFS
Triangolo LS
Tappeto g.
Tappeto IFS
Tappeto LS
Altri IFS.
Indice
Home
Contatti

©2003 - 2007 www.webfract.it