FRATTALE QUADRATICO DI CANTOR

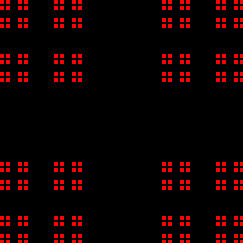
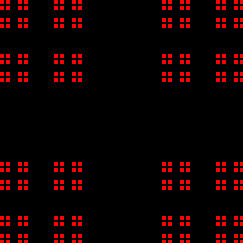
quadrato di Cantor

Questo è costruito seguendo il seguente metodo iterativo in cui il passo zero corrisponde alla figura di partenza non ancora trasformata:

  1. Prendiamo come figura di partenza un quadrato: poniamo per comodità la lunghezza del lato = 1
  2. Dividiamolo in nove parti uguali (dividiamo dunque ogni lato in tre parti uguali e conduciamo dai punti di divisione le parallele ai lati)
  3. Eliminiamo cinque quadrati lasciando soltanto i quattro quadrati d'angolo
  4. Ripetiamo il procedimento...

Otteniamo il frattale quadratico di Cantor, cosiddetto perché può essere costruito come prodotto cartesiano di  due insiemi di Cantor sui lati  adiacenti di un quadrato. Verifichiamo la nostra affermazione per il primo passo della costruzione:

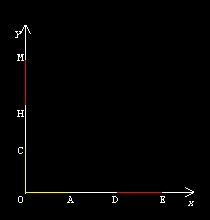Immaginiamo una curva di Cantor sull'asse x (che chiamiamo C1) ed una sull'asse y (che chiamiamo C2) di un piano cartesiano.
Immaginiamo che il segmento del passo zero, OE, misuri 3.
Avremo che:
0(0,0), A(1,0) ed il segmento OA è espresso dall'equazione 0<=x<=1 and y=0
D(2,0), E(3,0) ed il segmento OE è espresso dall'equazione 2<=x<=3 and y=0
0(0,0), C(0,1) ed il segmento OC è espresso dall'equazione x=0 and 0<=y<=1
H(0,2), M(0,3) ed il segmento HM è espresso dall'equazione x=0  and 2<=y<=3
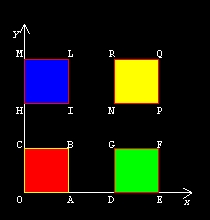Facciamo il prodotto cartesiano C1 × C2.
Come sappiamo, il prodotto cartesiano di due insiemi A × B è dato dall'insieme di tutte le coppie ordinate delle quali il primo elemento appartiene ad A ed il secondo a B.
Avremo allora che si formano i quattro quadrati illustrati in figura dei quali
il quadrato OABC è espresso dall'equazione 0<=x<=1 and 0<=y<=1;
il quadrato DEFG è espresso dall'equazione 2<=x<=3 and 0<=y<=1;
il quadrato HILM è espresso dall'equazione 0<=x<=1 and 2<=y<=3;
il quadrato NPQR è espresso dall'equazione 2<=x<=3 and 2<=y<=3.

La loro unione crea il frattale quadratico.

 

Il frattale quadratico di Cantor può essere anche così costruito:

si parte da un quadrato e lo si divide in 9 quadrati uguali;
si eliminano tutti i quadrati tranne i quattro quadrati agli angoli;
si ripete il procedimento;
quando il numero di passi tende all'infinito si ottiene il frattale quadratico di Cantor.

Nell'immagine a destra osserviamo il frattale di cantor al passo zero.
Cliccando su "Successivo" si può osservare lo sviluppo del frattale per i primi quattro passi
Cliccando su "Precedente" si può tornare indietro.

Ognuno dei quadrati ha area 1/9 del quadrato da cui è generato, mentre il loro numero si quadruplica: dunque l'area totale della figura è ogni volta i 4/9 dell'area precedente.
Al tendere dei passi all'infinito l'area del frattale quadratico di Cantor quindi tende a zero.
 

ALTRE CARATTERISTICHE

Precedente       Successivo


E' autosimile, infatti la struttura che osserviamo in scala normale viene ripetuta infinite volte all'interno della scala più piccola, e la possiamo ritrovare qualsiasi sia la potenza della lente d'ingrandimento che usiamo.
Ha dimensione non intera: osserviamo il primo passo della costruzione. Il frattale quadratico di Cantor è composto da 4 quadrati identici, il cui lato è 1/3 di quello del quadrato intero. Usando il metodo descritto per le figure autosimili, concludiamo che la dimensione è log 4 / log 3, circa 1,26.
L'insieme di Cantor presenta quindi pienamente le caratteristiche di un frattale.


 

Introduzione
Definizione

Realizzazione

Tipi di frattali
Caratteristiche
Curva di Cantor
 
Altri Iterativi
Indice
Home
Contatti

©2007 www.webfract.it