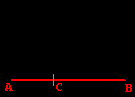
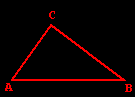
| Il terzo assioma della distanza ci assicura che, dati nel piano tre punti, A, B e C, AB ≤ AC + BC; il segno di uguaglianza vale se e soltanto se A, B e C sono allineati e C è compreso fra A e B. | |||||
|
|
 |
||||
|
AB = AC + BC |
AB < AC + BC (disuguaglianza triangolare) | ||||
|
Nel caso di un frattale, ad ogni passo, ogni singolo segmento
che lo compone subisce una
riduzione, d'altra parte il numero di segmenti aumenta: sostituiamo come
minimo due segmenti ad ognuno dei precedenti, e dunque la lunghezza complessiva,
per l'assioma della distanza, aumenta. Il processo di costruzione di un frattale si ripete all'infinito. Dunque il perimetro di una frattale tende ad infinito. |
|||||
|
|
|
|
|||
|
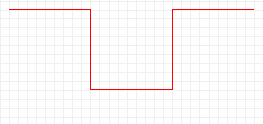
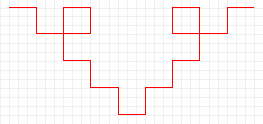
Inizio: 1 segmento di 27 quadretti |
Primo passo: 5 segmenti di 9 quadretti |
Secondo passo: 25 segmenti di 3 quadretti... |
|||
|
Mediante la legge di
formazione del frattale possiamo prevedere quanto sarà il perimetro al
passo successivo, e comunque è facile intuire che, al tendere dei passi ad
infinito, anche il perimetro tende ad infinito.
APPROFONDIMENTO Anche nella realtà il
concetto di lunghezza presenta dei limiti quando vogliamo
misurare una linea estremamente irregolare. |
|||||
|
|
|
|
|||
| Se misuriamo la distanza fra due punti in linea d'aria, troveremo una certa lunghezza. | Se misuriamo la distanza tra gli stesso due punti, ad esempio, a grandi passi, ecco che troviamo una lunghezza maggiore. | Più cerchiamo di aumentare la precisione e più la lunghezza aumenta. | |||
|
La lunghezza di un tratto di costa non potrà essere infinita, perché non
potremo dividere indefinitamente i tratti da misurare, ma l'andamento
delle successive misurazioni ricorda quello del calcolo del perimetro di
un frattale nei successivi passi. In effetti l'affermazione di Mandelbrot
voleva mettere in evidenza la natura dei frattali riferendosi all'immagine
familiare di una costa frastagliata. E' la matematica che garantisce l'esistenza effettiva dei frattali e delle loro proprietà caratteristiche. |
|||||