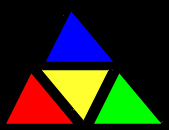
Come si vede dall'immagine a fianco, sono quattro i triangoli che possono comporre un triangolo con i lati ordinatamente doppi. Il triangolo ha infatti la dimensione di una superficie, e cioè due.
|
Applichiamo il concetto di dimensione appena introdotto al triangolo di Sierpinski, ricordando che, in generale,se n è il numero di ingrandimenti lineari, il numero di copie è rappresentato da una potenza di base n e di esponente la dimensione. Come si vede dall'immagine a fianco, sono quattro i triangoli che possono comporre un triangolo con i lati ordinatamente doppi. Il triangolo ha infatti la dimensione di una superficie, e cioè due.
| Raddoppiamo ora il lato di un triangolo di Sierpinski: ci si aspetterebbe di ottenere quattro copie dell'originale, invece esse sono soltanto tre. (Ricordiamoci di non contare i buchi!) | |
Impostiamo dunque l'equazione 3 = 2d dove d è la dimensione.
Ora, poiché 21 = 2, e 22 = 4, il nostro numero deve essere compreso fra 1 e 2.
Ecco in evidenza il paradosso apparente dei frattali: sono più di una linea ma meno di una superficie.
Se sai risolvere un'equazione esponenziale, otterrai facilmente che
d =log2 3 = log3/log2 = 1,5849625....
Altrimenti, potrai arrivare a questo valore per successive approssimazioni secondo il procedimento che segue.
NOTA BENE Non tutti i frattali, come vedremo, hanno dimensione frazionaria, tuttavia quello presentato è un ottimo metodo per scoprirlo.
|
| | |
©2002 www.webfract.it