PREMESSA

I numeri reali non bastano a risolvere tutti i problemi: ad esempio non esiste in R la radice quadrata di un numero negativo, poiché il quadrato di un numero reale è sempre positivo, se la base è diversa da zero, o nullo, quando è nulla. Dunque una semplice equazione di secondo grado come x2 + 1 = 0 non ammette soluzione nell'insieme dei numeri reali. Per ovviare a questo tipo di problemi di introduce l'unità immaginaria i che, elevata al quadrato, dà -1. Per analogia con i numeri reali, si ammette poi che anche (-i)2 = -1. Ecco allora che, ad esempio, un'equazione come x2 + 1 = 0 ammette le due soluzioni che ci aspettiamo: ± i.

× + - + + - - - + Regola dei segni

Risolviamo un'equazione del tipo x2 +2x + 5 = 0. Applicando la formula risolutiva troviamo le soluzioni -1 ± 2i. Ecco dunque che scopriamo numeri del tipo a+ib, cioè che hanno la forma di un binomio di primo grado in i e che prendono il nome di numeri complessi. Se un numero ha ha forma a+0i è reale: possiamo perciò dire che i numeri reali sono particolari numeri complessi. Le operazioni con i numeri complessi seguono le ordinarie regole dell'algebra; qui in particolare ci interessa calcolare il quadrato di un numero complesso: (a+ib)2 = a2 + 2bi + b2i 2 = (a2 - b2) + 2abi

RAPPRESENTAZIONE GEOMETRICA DEI NUMERI COMPLESSI

Fino alla fine del XVIII secolo i numeri complessi erano circondati da un alone di mistero. Ma ecco alcune considerazioni di Gauss:

1. Come ogni numero reale si può rappresentare con un punto di una rettaretta orientata.

   

   (Ad esempio, nell'immagine in alto, vediamo che ai numeri reali +3.5 e -4 corrispondono rispettivamente i punti P e Q, e viceversa.)

2. ogni numero complesso z = x + iy può essere allora rappresentato con un punto P di coordinate (x,y) di un piano (che, in suo onore, viene detto piano di Gauss).
   Esso si trova in corrispondenza biunivoca con il punto P(x,y).
   
   Ad esempio, nell'immagine a sinistra, vediamo che al numero complesso
   z = 2 + 4i corrisponde il punto P che ha come ascissa la parte reale, e come ordinata la parte immaginaria del numero.

MODULO DI UN NUMERO COMPLESSO

Dato il numero complesso in forma algebrica

z = x + iy

|z| = √x² + y²

Se indichiamo con P il punto, nel piano di Argand Gauss, che corrisponde a z, possiamo vedere che il modulo del numero complesso z rappresenta la lunghezza del segmento che congiunge P con l'origine.
Nella Figura 2., ad esempio, la distanza, che abbiamo indicato con d, del punto P dall'origine è

|z| = √2² + 4² = √20

OPERAZIONI CON I NUMERI COMPLESSI

Le operazioni con i numeri complessi seguono le ordinarie regole dell'algebra; qui in particolare ci interessa calcolare il quadrato di un numero complesso:

(a+ib)² = a² + 2bi + b²i ² = (a² - b²) + 2abi

Dunque il punto corrispondente ad (a+ib)² ha, nel piano di Gauss,

ascissa = a² - b²
ordinata = 2ab

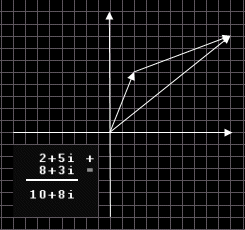
NUMERI COMPLESSI E VETTORI

Un numero complesso può essere pensato anche come un vettore: ad esempio al punto P possiamo far corrispondere il vettore OP ed al punto Q il vettore OQ.

Il modulo del numero complesso coincide, come sempre, con la lunghezza del vettore.
La somma di due numeri complessi è il vettore somma dei vettori che rappresentano i due numeri.

L'addizione di numeri complessi equivale quindi alla composizione di traslazioni che hanno come componenti rispettivamente la parte reale e la parte immaginaria dei numeri addendi.

Link utili: Polymath: appunti per una lezione - "I numeri complessi: un percorso didattico tra algebra e geometria" di Luigi Tomasi
             Clark University - "Dave's short course on complex numbers"

TORNA INDIETRO

©2002 - 2014 www.webfract.it