

DIMOSTRAZIONE
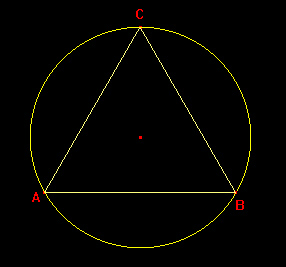
| Il triangolo è inscrivibile in un cerchio.
Il centro del cerchio circoscritto ad un triangolo è detto circocentro: esso è il punto di incontro degli assi dei lati.
| 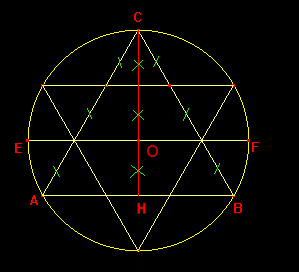
Dopo il primo passo |
La figura è costituita dall'unione di due triangoli equilateri uguali che sono simmetrici rispetto al diametro parallelo a ad un lato: ad esempio, nel disegno a fianco, i triangoli sono simmetrici rispetto al diametro EF, parallelo al lato AB.
| 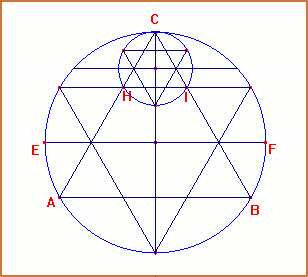
Dopo il secondo passo |
Dal triangolo equilatero HCI, come dagli altri, spuntano due triangoli equilateri. |
TROVIAMO UNA FORMULA PER L'AREA DEL FIOCCO DI NEVE
Ad ogni passo, si aggiungono al fiocco nuovi triangoli. Per valutare la loro area complessiva, dobbiamo determinare, di volta in volta:
Al passo 0 l'area vale S0| Al passo 1 si formano 3 triangoli di area 1/9 di S0 ciascuno.
|
| 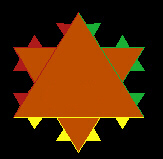
Al passo 2 si formano 3×4 triangoli di area 1/9 di 1/9 di S0 =S0/92. Quindi 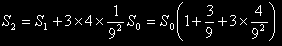
Al passo 3 si formano 3×42 triangoli di area 1/9 di 1/92 di S0 = S0/93. Quindi
|
Al passo k si formano 3×4k-1 triangoli di area S0/9k. Quindi
|
Il fiocco di neve è la figura limite che si ottiene reiterando il procedimento all'infinito. | Per questo, occorre trovare il limite di Sk per k che tende all'infinito. Tale limite si calcola facilmente ove si noti la presenza, nelle somme parziali, di una serie geometrica di ragione 4/9 e di termine iniziale 3/9.
Ricordando la formula che esprime l'area di un triangolo equilatero di lato s si ottiene finalmente
|
| |||||||||||||
| Indice | Home | Scrivi |
©2003 www.webfract.it