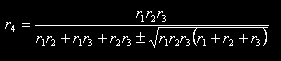
PREMESSA
Consideriamo 3 cerchi tangenti a due a due e di centri rispettivamente A(x1,y1),
B(x2,
y2),
C(x3,y3) e di raggi r1, r2, r3.
Vogliamo calcolare centro D(x4,y4) e raggio r4 del cerchio
interno tangente a tutti e tre i cerchi.
Calcoliamo r4 mediante la seguente formula, dovuta a Frederick Soddy (biografia su Wikipedia):
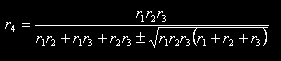
Nella formula scegliamo il segno + davanti alla radice, infatti il segno - si riferisce al cerchio esterno tangente ai tre cerchi.
La formula si ricava direttamente dal teorema di Cartesio (approfondimento su Wikipedia):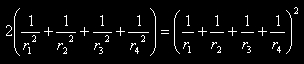
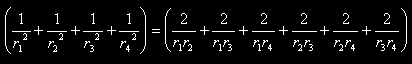
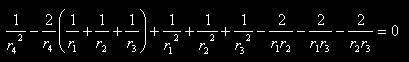
Sappiamo inoltre che, nel caso di due cerchi tangenti esternamente vale la proprietą che la distanza fra i centri č uguale alla somma dei raggi.
Possiamo dunque scrivere (abbiamo omesso le graffe):
Sottraendo membro a membro la B. dalla A. e la C. dalla B. e svolgendo i calcoli otteniamo (abbiamo omesso le graffe):
-2x4(x1-x2)-2y4(y1-y2) = r12-r22+2r4 (r1-r2)-x12+x22-y12+y22
-2x4(x2-x3)-2y4(y2-y3) = r22-r32+2r4 (r2-r3)-x22+x32-y22+y32
Si tratta di risolvere un sistema lineare di 2 equazioni in 2 incognite (x4 e y4), compito che lasciamo volentieri al computer.
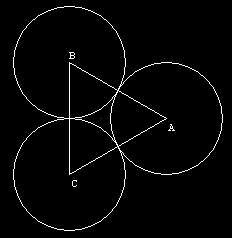 Le tre circonferenze, CA, CB, CC, mutuamente tangenti, tutte di raggio √3/2, hanno centro rispettivamente in
Le tre circonferenze, CA, CB, CC, mutuamente tangenti, tutte di raggio √3/2, hanno centro rispettivamente in
A(1,0)
B(-1/2, +√3/2)
C(-1/2, -√3/2).
Tali punti sono i vertici di un triangolo equilatero inscritto in un cerchio di raggio 1.
Disegniamo le tre circonferenze.
Prepariamo una procedura ricorsiva, di nome apollo, alla quale dovremo passare ordinatamente, come parametri:
Se n = 0 allora
disegna il cerchio di raggio ra e centro xa e ya
altrimenti
raggio = (ra * rb * rc) / (ra * rb + rb * rc + ra * rc + 2 * Sqr(ra * rb * rc * (ra + rb + rc)))
a1S = -2 * (xb - xc)
b1S = -2 * (yb - yc)
c1S = rb ^ 2 - rc ^ 2 + 2 * raggio * (rb - rc) + xc ^ 2 - xb ^ 2 + yc ^ 2 - yb ^ 2
a2S = -2 * (xa - xb)
b2S = -2 * (ya - yb)
c2S = ra ^ 2 - rb ^ 2 + 2 * raggio * (ra - rb) + xb ^ 2 - xa ^ 2 + yb ^ 2 - ya ^ 2
Se (a1S * b2S - a2S * b1S <> 0) allora
x0 = (b2S * c1S - b1S * c2S) / (a1S * b2S - a2S * b1S)
y0 = (a1S * c2S - a2S * c1S) / (a1S * b2S - a2S * b1S)
Fine se
xaT = x0
yaT = y0
raT = raggio
xbT = x0
ybT = y0
rbT = raggio
xcT = x0
ycT = y0
rcT = raggio
Chiama apollo(n - 1, xa, ya, ra, xb, yb, rb, xcT, ycT, rcT)
Chiama apollo(n - 1, xa, ya, ra, xbT, ybT, rbT, xc, yc, rc)
Chiama apollo(n - 1, xaT, yaT, raT, xb, yb, rb, xc, yc, rc)
Fine se
Torna al frattale di Apollonio
©2008 www.webfract.it