Partiamo da un punto P0(x + iy) nel piano complesso e applichiamo la seguente trasformazione: z0 = 3 / (1 + √3 - z) + (1 - √3)      dove z = x+iy e z0 = x0+iy0 La trasformazione si può ottenere mediante la simmetria assiale rispetto alla retta di equazione x=1 seguita dall'inversione circolare rispetto al cerchio di centro C((1 - √3), 0) e raggio √3 Svolgendo i calcoli otteniamo: 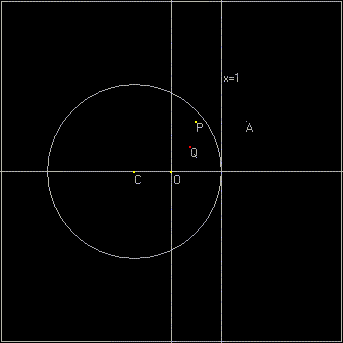Nell'immagine a fianco il punto P si trasforma prima nel punto A e quindi nel punto Q. Cliccando sui collegamenti si possono visualizzare o il trasformato di un grigliato in cui ad ogni segmento corrisponde la curva con lo stesso colore, o un suo ingrandimento; oppure si torna all'immagine attuale.

Trasformato di un grigliato      Ingrandimento      Trasformato di un punto

1°	z1 = z0 Svolgendo i calcoli otteniamo: x1 = x0 y1 = y0
2°	z1 = 1/z0(-1 + i√3) Si tratta di comporre le seguenti trasformazioni: Simmetria rispetto all'asse reale; inversione circolare rispetto al cerchio con centro nell'origine e raggio unitario; rotazione di 120° con centro nell'origine Svolgendo i calcoli otteniamo: Posto D = x02 + y02 Tx = x0 / D Ty = -y0 / D a1 = -1/2 b1 = √3 Si ha: x1 = Txa1 - Tyb1 y1 = Txb1 + Tya1 Nell'immagine a fianco possiamo vedere come agisce la seconda trasformazione sullo stesso grigliato che abbiamo usato prima.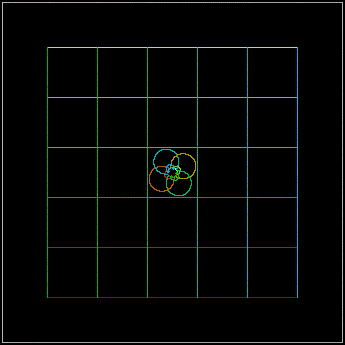
Cliccando sui collegamenti si possono visualizzare o un suo ingrandimento o la trasformazione completa a partire dal punto P(x+iy); oppure si torna all'immagine attuale. Ingrandimento      Trasformazione completa      Immagine di partenza
3°	z1 =1/z0(-1 - i√3) Si tratta di comporre le seguenti trasformazioni: Simmetria rispetto all'asse reale; inversione circolare rispetto al cerchio con centro nell'origine e raggio unitario; rotazione di 240° con centro nell'origine Svolgendo i calcoli otteniamo: Posto D = x02 + y02 Tx = x0 / D Ty = -y0 / D a2 = -1/2 b2 = -√3 Si ha: x1 = Txa2 - Tyb2 y1 = Txb2 + Tya2 Nell'immagine a fianco si visualizza la trasformazione completa a partire dal punto P(x+iy)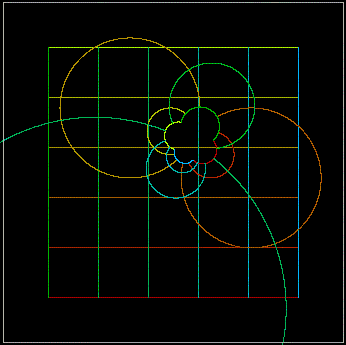

Al tendere dei passi all'infinito l'area del setaccio di Apollonio tende a zero mentre il perimetro tende ad infinito.
Non essendo la figura autosimile, non possiamo calcolare la sua dimensione con il metodo descritto per le figure autosimili, tuttavia la sua dimensione è stata calcolata ed è circa 1.3058 (Mandelbrot 1983, p. 172)

Listato del programma